Single factor phenotypic model: 4 arithmetic computation variables Data NGroups=1 NInput_vars=4 NObservations=42 CMatrix 259.664 209.325 259.939 209.532 220.755 245.235 221.610 221.491 221.317 249.298 Labels Time1 Time2 Time3 Time4 Begin Maces; B Full 1 4 Free P Symm 1 1 E Diag 4 4 Free End Matrices Value 1 P 1 1 Start 9 All Covariances B*P*B'+E; Option RSidual End
The parameters in the group type statement indicate that we
have only NGroup=1 group (consisting of NObservations=42
subjects) and there are NInput_vars=4 input variables. The
loadings of the four variables on the single common factor are
estimated in matrix B and their specific variances are estimated
on the diagonal of matrix E. In this phenotypic factor model,
we have sufficient information to estimate factor loadings and
specific variances for the four variables, but we cannot
simultaneously estimate the variance of the common factor because the
model would then be underidentified. We therefore fix the variance of
the latent factor to an arbitrary non-zero constant, which we choose
to be unity in order to keep the factor loadings and specific
variances in the original scale of measurement (Value 1 P 1 1).
The Mx output (after editing) from this common factor model is shown
below. The PARAMETER SPECIFICATIONS section of the output
depicts the single common factor structure of the model: there are
free factor loadings for each of the four variables on the common
factor, and specific variance parameters for each of the observed
variables. Thus, the model has a total of 8 parameters to explain the
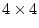free statistics. The chi-squared goodness-of-fit
value of 1.46 for 2 degrees of freedom suggests that this single
factor model adequately explains the observed covariances ( =
.483). This also may be seen by comparing the elements of the fitted
covariance matrix and the observed covariance matrix, which are seen
to be very similar. The fitted covariance matrix is printed by Mx
when the RSiduals option is added. The fitted covariance
matrix is calculated by Mx using expression 10.2 with the
final estimated parameter values.