Using genetic notation, the genetic factor model can be represented as
In Mx, there are a number of alternative ways to specify the model.
One approach is to specify the factor structure for the genetic,
shared and specific environmental factors in one matrix, e.g. B
with twice the number of variables (for both twins) as rows and the
number of factors for each twin as columns. If we assume one genetic,
one shared environmental and one specific environmental common factor
per twin
![]() for our four-variate
arithmetic computation example (shown as T0 - T3 to represent
administration times 0-3 before and after standard doses of alcohol
for twin 1 (Tw1) and twin 2 (Tw2) respectively), the B matrix
would look like
for our four-variate
arithmetic computation example (shown as T0 - T3 to represent
administration times 0-3 before and after standard doses of alcohol
for twin 1 (Tw1) and twin 2 (Tw2) respectively), the B matrix
would look like
In this case with 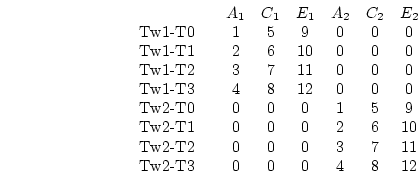 factors and four observed variables for each
twin (p=8), B would be a
factors and four observed variables for each
twin (p=8), B would be a ![]() (
(![]() ) matrix of the
factor loadings, P the
) matrix of the
factor loadings, P the ![]() correlation matrix of factor
scores, and E a
correlation matrix of factor
scores, and E a  diagonal matrix of unique
variances. The
expected covariance may then be calculated as in
equation 10.1:
diagonal matrix of unique
variances. The
expected covariance may then be calculated as in
equation 10.1:
| (61) |
In a multivariate analysis of twin data according to this factor
model, ![]() is a
is a ![]() predicted covariance matrix of
observations on twin 1 and twin 2 and B is a
predicted covariance matrix of
observations on twin 1 and twin 2 and B is a ![]() matrix of loadings of these observations on latent genotypes and
non-shared and common environments of twin 1 and twin 2. The factor
loadings between
matrix of loadings of these observations on latent genotypes and
non-shared and common environments of twin 1 and twin 2. The factor
loadings between ![]() and
and ![]() ,
, ![]() and
and ![]() , and
, and 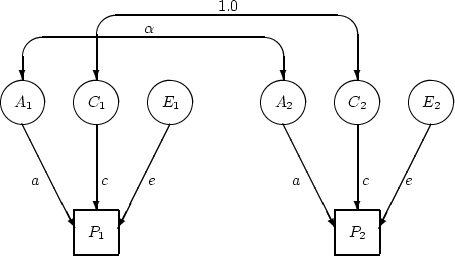 and
and ![]() are constrained to be equal for twin 1 and twin 2, similar to the path
coefficients of the univariate models discussed in previous chapters.
The equality constraints on the parameters are obtained in Mx by using
the same non-zero parameter number in a
are constrained to be equal for twin 1 and twin 2, similar to the path
coefficients of the univariate models discussed in previous chapters.
The equality constraints on the parameters are obtained in Mx by using
the same non-zero parameter number in a Specification statement
for the free parameters. The unique variances also are equal for both
members of a twin pair. These may be estimated on the diagonal of the
![]() E matrix (e.g., Heath et al., 1989c). To fit this model, B and bf
E are estimated from the data and P (
E matrix (e.g., Heath et al., 1989c). To fit this model, B and bf
E are estimated from the data and P (![]() ) must be
fixed a priori (for example, the correlation between
) must be
fixed a priori (for example, the correlation between ![]() for
twin 1 and
for
twin 1 and ![]() for twin 2 is 1.0 for MZ and 0.5 for DZ twins; the
correlation between the
for twin 2 is 1.0 for MZ and 0.5 for DZ twins; the
correlation between the ![]() variables of twin 1 and twin 2 is 1.0).
variables of twin 1 and twin 2 is 1.0).
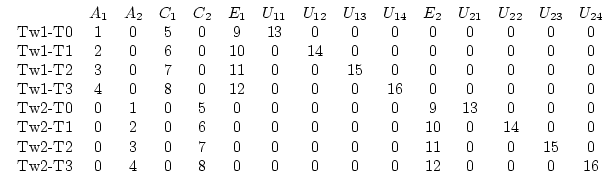
One alternative specification of this model is to include the unique
variances in matrix B and fix E to zero. We have omitted
the shared environmental component.
Close inspection of this matrix reveals that the factor patterns for
![]() and
and ![]() of twin 1 and twin 2 are identical to that in
Section 10.2.3. The main difference lies in the treatment of the
unique variances. In the earlier example these were estimated as
variances on the diagonal of E, but now they are modeled as the
square roots of the variances. These quantities are now square
roots because the unique variances are calculated as the product
of twin 1 and twin 2 are identical to that in
Section 10.2.3. The main difference lies in the treatment of the
unique variances. In the earlier example these were estimated as
variances on the diagonal of E, but now they are modeled as the
square roots of the variances. These quantities are now square
roots because the unique variances are calculated as the product
 in the expected covariance expression whereas in the
previous example the quantities were estimated as the unproducted
quantity E. One might expect that this subtle change would have
no effect on the model (as indeed it does not in this example), but on
occasion these alternative residual specifications may produce
different outcomes. The situation of residual variances
in the expected covariance expression whereas in the
previous example the quantities were estimated as the unproducted
quantity E. One might expect that this subtle change would have
no effect on the model (as indeed it does not in this example), but on
occasion these alternative residual specifications may produce
different outcomes. The situation of residual variances ![]() makes
little sense in genetic analyses because it implies an impossible
negative variance component. Consequently, although it may be
possible to make alternative representations like this in Mx, we
recommend this model, as it constrains unique variances to be
makes
little sense in genetic analyses because it implies an impossible
negative variance component. Consequently, although it may be
possible to make alternative representations like this in Mx, we
recommend this model, as it constrains unique variances to be ![]() . Nevertheless, both methods give identical solutions when fitted
to the data used in these examples.
. Nevertheless, both methods give identical solutions when fitted
to the data used in these examples.