1 Matrix Notation

Many people regard journal articles and books that contain matrix algebra as prohibitively complicated and ignore them or shelve them indefinitely. This is a sad state of affairs because learning matrix algebra is not difficult and can reap enormous benefits. Science in general, and genetics in particular, is becoming increasingly quantitative. Matrix algebra provides a very economical language to describe our data and our models; it is essential for understanding Mx and other data analysis packages. In common with most languages, the way to make it ``stick'' is to use it. Those unfamiliar with, or out of practice at, using matrices will benefit from doing the worked examples in the text. Readers with a strong mathematics background may skim this chapter, or skip it entirely, using it for reference only. We do not give an exhaustive treatment of matrix algebra and operations but limit ourselves to the bare essentials needed for structural equation modeling. There are many excellent texts for those wishing to extend their knowledge; we recommend Searle (1982) and Graybill (1969).

Although matrices and certain matrix operations were used as long ago as 2000 BC in ancient China, it is only relatively recently that a comprehensive matrix algebra has been developed. During the 1850's, Cayley worked on general algebraic systems (Boyer, 1985 p. 627) and developed the basis of matrix algebra as it is used today. The concept of a matrix is a very simple one, being just a table of numbers or symbols laid out in rows and columns,

$$\mbox{e.g.,} \left( \begin{array}{rr} 1 & 4\\ 2 & 5\\ 3 ... ..._{22} & a_{23}\\ a_{31} & a_{32} & a_{33} \end{array} \right)$$

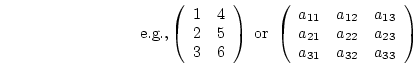In most texts, the table is enclosed in brackets, either: curved, $\left( \right)$; square, $\left[ \; \right]$; or curly, $\left\{ \right\}$.

It is conventional to specify the configuration of the matrix in terms of Rows $\times$ Columns and these are its dimensions or order. Thus the first matrix above is of order 3 by 2 and the second is a $3 \times 3$ matrix.

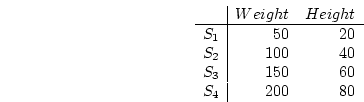
A common occurrence of matrices in behavioral sciences is the data matrix where the rows are subjects and the columns are measures, e.g.,

$$\begin{array}{l\vert rr} & Weight & Height\\ \hline S_{1} &... ...0 & 40\\ S_{3} & 150 & 60\\ S_{4} & 200 & 80\\ \end{array}$$

It is convenient to let a single letter symbolize a matrix. This is written in UPPERCASE boldface. Thus we might say that our data matrix is A, which in handwriting we would underline with either a straight or a wavy line. Sometimes a matrix is written $_{4}{\bf A}_{2}$ to specify its dimensions. The economy of using matrices is immediately apparent: we can represent a whole table by a single symbol, whether it contains just one row and one column, or a billion rows and a billion columns! There are several special terms for matrices with one row or one column or both. When a matrix consists of a single number, it is called a scalar; when it consists of single column (row) of numbers it is called a column (row) vector. Scalars are usually represented as lower case, non-bold letters. Vectors are normally represented as a bold lowercase letter. Thus, the weight measurements of our four subjects are

$$\left[ \begin{array}{r} 50\\ 100\\ 150\\ 200\\ \end{array} \right] = {\bf a}$$

We can refer to the specific elements of matrix $\bf A$ as $a_{ij}$ where $i$ indicates the row number and $j$ indicates the column number.

Certain special forms of matrices exist. We have already defined scalars and row and column vectors. A matrix full of zeroes is called a null matrix and a matrix full of ones is called a unit matrix. Matrices in which the number of rows is equal to the number of columns are called square matrices. Among square matrices, diagonal matrices have at least one non-zero diagonal element, with every off-diagonal element zero. By diagonal, we mean the `leading diagonal' from the top left element of the matrix to the bottom right element. A special form of the diagonal matrix is the identity matrix, I, which has every diagonal element one and every non-diagonal element zero. The identity matrix functions much like the number one in ordinary algebra.