



Next: 3 Matrix Algebra Operations
Up: 4 Matrix Algebra
Previous: 1 Introduction
Index
2 Matrix Notation
Although matrices and certain matrix operations were used as long ago
as 2000 BC in ancient China, it is only relatively recently that a
comprehensive matrix algebra has been developed. During the 1850's,
Cayley worked on general algebraic systems (Boyer, 1985 p. 627)
and developed the basis of matrix algebra as it is
used today. The concept of a matrix is a very simple one, being just
a table of numbers or symbols laid out in rows and
columns,
In most texts, the table is enclosed in brackets, either: curved,
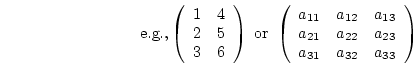 ; square,
; square,
![$\left[ \; \right]$](img331.png) ; or curly,
; or curly,
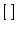 .
It is conventional to specify the configuration of the matrix in terms
of Rows
.
It is conventional to specify the configuration of the matrix in terms
of Rows  Columns and these are its dimensions or
order. Thus the first
matrix above is of order 3 by 2 and the second is a
Columns and these are its dimensions or
order. Thus the first
matrix above is of order 3 by 2 and the second is a 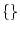 matrix.
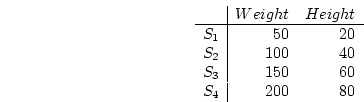
A common occurrence of matrices in behavioral sciences is the data
matrix where the rows are
subjects and the columns are measures, e.g.,
matrix.
A common occurrence of matrices in behavioral sciences is the data
matrix where the rows are
subjects and the columns are measures, e.g.,
It is convenient to let a single letter symbolize a matrix. This is
written in UPPERCASE boldface. Thus we might say that our data
matrix is A, which in handwriting we would underline with either
a straight or a wavy line. Sometimes a matrix is written
 to specify its dimensions. The economy of using matrices is
immediately apparent: we can represent a whole table by a single
symbol, whether it contains just one row and one column, or a billion
rows and a billion columns! There are several special terms for
matrices with one row or one column or both. When a matrix consists
of a single number, it is called a scalar;
when it consists of single column (row) of numbers it is called a
column (row) vector. Scalars are usually
represented as lower case, non-bold letters. Vectors are normally
represented as a bold lowercase letter. Thus, the weight
measurements of our four subjects are
to specify its dimensions. The economy of using matrices is
immediately apparent: we can represent a whole table by a single
symbol, whether it contains just one row and one column, or a billion
rows and a billion columns! There are several special terms for
matrices with one row or one column or both. When a matrix consists
of a single number, it is called a scalar;
when it consists of single column (row) of numbers it is called a
column (row) vector. Scalars are usually
represented as lower case, non-bold letters. Vectors are normally
represented as a bold lowercase letter. Thus, the weight
measurements of our four subjects are
We can refer to the specific elements of matrix  as
as 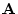 where
where 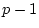 indicates the row number and
indicates the row number and 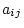 indicates the column
number.
Certain special forms of matrices exist. We have already defined
scalars and row and column vectors. A matrix full of zeroes is called
a null matrix and a matrix full of ones is
called a unit matrix. Matrices in which the
number of rows is equal to the number of columns are called
square matrices. Among square matrices,
diagonal matrices have at least one non-zero
diagonal element, with every off-diagonal element zero. By diagonal,
we mean the `leading diagonal' from the top left element of the matrix
to the bottom right element. A special form of the diagonal matrix is
the identity matrix, I, which has
every diagonal element one and every non-diagonal element zero. The
identity matrix functions much like the number one in ordinary
algebra.
indicates the column
number.
Certain special forms of matrices exist. We have already defined
scalars and row and column vectors. A matrix full of zeroes is called
a null matrix and a matrix full of ones is
called a unit matrix. Matrices in which the
number of rows is equal to the number of columns are called
square matrices. Among square matrices,
diagonal matrices have at least one non-zero
diagonal element, with every off-diagonal element zero. By diagonal,
we mean the `leading diagonal' from the top left element of the matrix
to the bottom right element. A special form of the diagonal matrix is
the identity matrix, I, which has
every diagonal element one and every non-diagonal element zero. The
identity matrix functions much like the number one in ordinary
algebra.




Next: 3 Matrix Algebra Operations
Up: 4 Matrix Algebra
Previous: 1 Introduction
Index
Jeff Lessem
2002-03-21
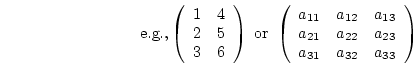 ; square,
; square,
 to specify its dimensions. The economy of using matrices is
immediately apparent: we can represent a whole table by a single
symbol, whether it contains just one row and one column, or a billion
rows and a billion columns! There are several special terms for
matrices with one row or one column or both. When a matrix consists
of a single number, it is called a scalar;
when it consists of single column (row) of numbers it is called a
column (row) vector. Scalars are usually
represented as lower case, non-bold letters. Vectors are normally
represented as a bold lowercase letter. Thus, the weight
measurements of our four subjects are
to specify its dimensions. The economy of using matrices is
immediately apparent: we can represent a whole table by a single
symbol, whether it contains just one row and one column, or a billion
rows and a billion columns! There are several special terms for
matrices with one row or one column or both. When a matrix consists
of a single number, it is called a scalar;
when it consists of single column (row) of numbers it is called a
column (row) vector. Scalars are usually
represented as lower case, non-bold letters. Vectors are normally
represented as a bold lowercase letter. Thus, the weight
measurements of our four subjects are
 as
as