1.0: Introduction.

Just as ordinary genetic analysis of simple traits can require elaborate mathematical models, so does the analysis of behavioral data. This handout is meant as a simple and nontechnical introduction to the fundamental techniques currently used in behavioral genetics. Like all such mathematical writings, it becomes very easy for the student to fall into the ìforest for the treesî syndrome. In reading this, concentrate on the larger issue of the types of questions that behavioral genetics are asking and less on the mechanics of how to go about answering those questions. If you can successfully do the problems at the end of this chapterónot from memorizing the formula, but from knowing where to look the formula up in this handoutóthen you will have mastered the material successfully.

2.0: Heritability and Environmentability

The concepts of heritability and environmentability are central to quantitative analysis in behavioral genetics. Instead of providing formal definitions of these terms, let us begin with a simple thought experiment and then discover the definitions through induction.

Imagine that scores on the behavioral trait of impulsivity are gathered on a whole population of individuals. These observed scores will be called the phenotypic values of the individuals. Assume that there was a futuristic genetic technology that could genotype all of the individuals in this population for all the loci that contribute to impulsivity. One could then construct a genotypic value for each individual. The genotypic value of an individual is defined as the mean phenotypic value of all those individuals with that genotype in the population. For example, if Wilbur Waterschmeltzerís genotype for impulsivity is AaBBCCddEeff and the mean impulsivity score for all individuals in the population who have genotype AaBBCCddEeff is 43.27, then Wilburís genotypic value is 43.27.

Imagine another technical advance that would permit us to calculate and quantify all the environmental experiences in a personís life that would contribute to the personís level of impulsivity. This would be the environmental value for an individual. We would then have a very large set of data, the initial part of which would resemble Table 1.

Table 1. Hypothetical data set containing the phenotypic, genetic, and environmental values for individuals.
Observation	Genetic Value = G	Environmental Value = E	Phenotypic Value = P
Abernathy Abercrombie	113	96	107
Beulah Bellingwacker	92	74	77
Ö	.	.	.
Zelda Zorkminder	118	104	118

We could then compute a correlation coefficient between the genotypic values and the phenotypic values. Recall that the square of the correlation coefficient between two variables gives the proportion of variance in one variable attributable to (i.e., predicted by) the other variable. Consequently, if we square the correlation coefficient between the genotypic values and the phenotypic values, we would arrive at the proportion of phenotypic variance predicted by (or attributable to) genetic variance. This quantity, the square of the correlation coefficient between genotypic values and phenotypic values, is called heritability.

Thus, heritability is a quantitative index of the importance of genetics for individual differences in a phenotype. Its strict statistical definition is the proportion of phenotypic variance attributable to or predicted by genetic variance. Because heritability is a proportion, it will range from 0 to 1.0. A heritability of 0 means that there is no genetic influence on a trait, whereas a heritability of 1.0 mean that trait variance is due solely to heredity. A less technical definition of heritability is that it is a measure, ranging from 0 to 1.0, of the extent to which observed individual differences can be traced in any way to genetic individual differences.

Just as we could compute a correlation between genetic values and phenotypic values, we could also compute correlations between environmental values and phenotypic values. Squaring this correlation would give us the environmentability of the trait. Environmentability has the same logical meaning as heritability but applies to the environment instead of the genes. Environmentability is the proportion of phenotypic variance attributable or predicted by environmental variance. It is also a quantitative index, ranging from 0 to 1.0, of the extent to which environmental individual differences underlie observable, phenotypic individual differences.

Figure 1: Example of a path diagram.

3.0: Path Analysis

At this point, it will be helpful to postpone further discussion of heritability and environmentability in favor of introducing a mathematical technique called path analysis. Path analysis depicts a mathematical model that is hypothesized to explain the correlations among variables. The technique was originally developed by Sewall Wright to solve intricate genetic problems. It has since been adopted by virtually all the behavioral sciences and applied to a large number of nongenetic research questions.

Path analysis begins with a path diagram that consists of a number of measured (i.e., observed) variables and unmeasured (i.e., latent) variables connected together by single-headed and double-headed arrows. Figure 1 gives an illustration of a path diagram for the hypothetical data described above involving genotypic, environmental, and phenotypic values.

3.1: Types of variables in path analysis

Latent, unmeasured, or unobserved variables are denoted in path analysis by enclosing them in a circle. Because we cannot directly observe and measure the genotypes and environments, the G and E variables in Figure 1 are latent variables and thus have circles around them. Manifest, measured or observed variables are enclosed in rectangles or squares. Because phenotypes are measured, P is enclosed in a rectangle in Figure 1.

In addition to the distinction between measured and unmeasured variables, there is a second distinction between variables in path analysis. Any variable with a single-headed arrow going into it is termed an endogenous variable. Any variable without an single-headed arrow going into it is termed an exogenous variable. One exogenous variable may be joined to another exogenous variable by a double-headed arrow. However, a double-headed arrow can never be used with an endogenous variable. In Figure 1, G and E are exogenous variables. P is an endogenous variables.

3.2: The meaning of the arrows in path analysis.

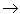
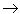
A single-headed arrow has two different meanings in path analysis, a strong meaning and a weak meaning. In the strong meaning, a single-headed arrow denotes causality. Thus A B signifies that A causes B. The weak meaning treats the single-headed arrow only in a statistical sense. A single-headed arrow denotes only direct predictability with no commitment made about causality. In this sense, A B denotes that individual differences in variable A can still predict individual differences in variable B even when all other variables that predict B are taken into account.

A double-headed arrow denotes a correlation between two exogenous variables. No commitment is made about either causality or direct predictability. Thus, A 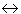B simply means that A is correlated with B. It may be that A causes B, or B causes A, or both cause each other, or there is a very complicated causal network that ultimately results in A being correlated with B. In Figure 1, the there is a correlation between the genotypic values and the environmental values. The reasons for this correlation may be quite complicated, but all the path model assumes is that individuals with high genotypic values may also have high environmental values. This path model makes no commitment as to the source of this similarity.

3.3: Path coefficients

The quantities h, e, and r in Figure 1 are termed path coefficients. They quantify the magnitude of a correlation, a cause, or a direct prediction. For example, the h on the single-headed arrow between G and P in Figure 1 quantifies the effect to which genes produce individual differences in the phenotype (strong interpretation) or the extent to which genetic individual differences directly predict phenotypic individual differences (weak interpretation). If h is large, then a great deal of phenotypic individual differences are caused by (strong interpretation) or directly predicted by (weak interpretation) genetic individual differences. If h is small, then genes have only a minor influence (strong interpretation) or weakly predict (weak interpretation) individual differences.

3.4: Purpose of path analysis

The whole purpose of path analysis is to use the correlations between the observed variables to obtain estimates of the path coefficients. It is also possible to use path analysis to perform statistical tests about whether certain path coefficients are significantly different than 0. For example, with the correct data, one could use the model in Figure 1 to test if the path coefficient h is significantly greater than 0. This is how behavioral geneticists determine whether or not heredity influences phenotypes such as cognitive abilities, personality, psychopathology, and so on. To perform this type of test, one must first learn how to derive the predicted correlation between observed variables in a path diagram.

3.5: Deriving predicted correlations

Predicted correlations for a path model may be derived from following four rules. They are:

1. Start with a predicted correlation of 0.

2. Trace a legitimate pathway, that has not been traversed before, between the two observed variables, multiplying the coefficients as you go.

3. Sum the results of step 2 to the predicted correlation

4. Repeat steps 2 and 3 until all the different pathways have been traversed.

These rules can be easily applied once one knows what a legitimate pathway is. It is actually easier to define an illegitimate or illegal pathway and then state that a legitimate or legal pathway is simply not an illegal pathway. An illegitimate or illegal pathway is one that enters a variable on an arrowhead and then exits that variable on an arrowhead. For example, in Figure 1, it is illegal to go from G to P via path h and then to go from P ro E via path e. The reasons is that we have entered variable P on an arrowhead and hence, cannot exit variable P on an arrowhead.

To illustrate these rules, consider Figure 1 and calculate the correlation between genotypic values and environmental values. First, we set R_GP = 0 and we will start with G and find all the paths to P. The first way is to straight to P from G via path h. Adding this to the value for R_GP gives R_GP = h. The second path is to go from G to E via the double-headed arrow r and then from E to P via path e, giving the quantity re. Thus, the correlation between genotypic and phenotypic values is R_GP = h + re.

Using similar path rules, we would calculate the correlation between environmental values and phenotypic values. The first path goes directly from E to P via e, and the second pathway goes from E to G then to P giving rh. Thus, the correlation between environment and phenotypic values is R_EP = e + rh.

4.0: Sibling resemblance and the twin method

It is not possible to estimate heritability and environmentability directly because it is unfeasible to obtain genotypic and environmental values. Consequently, in practice, these quantites are indirect estimated, typically through the use of the twin and the adoption methods.

Because twins are a special type of siblings, we start with Figure 2 which gives a path model for the resemblance for sib-pairs. The subscripts 1 and 2 are used to denote the first and second member of the sib-pairs, so P₁ denotes the phenotypic values for sib 1, G₂ denotes genotypic values for sib 2, etc.. In addition to the familiar path coefficients h and e, there are two new correlations on the double-headed arrows. The first of these, g, gives the correlation between the genotypes of the sib-pairs. The second of them, h, gives the correlation between the environmental values of the sib-pairs. The hypothetical data set that might be used to for this path model is illustrated in Table 2. The data are similar in structure to that in Table 1 with one important exception. In Table 2, the unit of observation is now the family, not a single individual.

Table 2. Hypothetical genotypic (G), environmental (E), and phenotypic (P) values for a series of sib-pairs.
	Sib 1			Sib 2
Sib-Pair	G1	E1	P1	G2	E2	P2
Athabaska Twins	113	96	107	101	108	106
Bottomwinger Twins	92	74	77	103	113	104
Ö	.	.	.	.	.	.
Zakmeister Twins	118	104	118	99	89	102

Let us return to the main task--that of finding the predicted correlation between the two observable variables in Figure 2, P₁ and P₂. Let the predicted correlation be denoted as R_sibs. We start by letting R_sibs = 0. The first pathway between P₁ and P₂ goes from P₁ to G₁ (via h), then from G₁ to G₂ (via g), and then from G₂ to P₂ (via h). Multiplying the coefficients together gives gh², so the predicted correlation thus far for siblings is gh². The second pathway between P₁ and P₂ starts at P₁, goes to E₁ then to E₂ and then to P₂. The coefficients for this pathway are e, h, and e which, when multiplied together, give he². Adding this to the predicted correlation for sibs gives R_sibs = gh² + he². Because there are no more pathways between P₁ and P₂, the final, predicted correlation between siblings gives

Figure 2. Path diagram for the relationship between two siblings.

G1 = genotypic value for sib 1; E1 = environmental value for sib 1; P1 = phenotypic value for sib 1. G2, E2, and P2 = genotypic, environmental and phenotypic values for sib 2.

5.1: The unknown value of g.

Here, a small digression is in order because the quantity g in the path model for siblings requires some explanation. This quantity is the correlation between the genotypic values of siblings. If the siblings are identical twins, then g = 1.0 because the twins have identical genotypes. For fraternal twins and for ordinary siblings, the precise mathematical value of g is not known. If the world of genetics were a simple place where each allele merely added or subtracted a small value from the phenotype and there were no assortative mating for the trait, then g would equal .50. This value of g is often assumed in the analysis of actual data, more for the sake of mathematical convenience than for substantive research demonstrating that the assumptions for choosing this value are valid.

If gene action is not simple and additive, then the value of g will be something less than .50. The two classic types of nonadditive gene action are dominance and epistasis. Dominance, of course, occurs when the phenotypic value for a heterozygote is not exactly half way between the phenotypic values of the two homozygotes. Epistasis occurs when there is a statistical interaction between genotypes. Both dominance and epistasis create what is termed nonadditive genetic variance. For technical reasons, nonadditive genetic variance reduces the correlation between siblings to something less than .50.

Assortative mating, on the other hand, will tend to increase the value of g. When parents are phenotypically similar and when there is some heritability, then the genotypes of parents will be correlated. The effect of this is to increase the genetic resemblance of their offspring over and above what it would be under random mating.

What should be done under such complexities? The typical strategy of setting g equal to .50 is not a bad place to start. If a trait shows strong assortative mating, then more elaborate mathematical models can be developed to account for the effects of nonrandom mating. The real problem occurs with nonadditive genetic variance. When this is present, then the techniques described above can overestimate heritability. This is another reason why heritability estimates should not be interpreted as precise, mathematical quantities.

5.2. Twins raised together

Let us return to the topic of the twin design. The correlation for siblings is:

If the siblings are identical twins, then g = 1 and the correlation can be written as

The twin method makes the assumption that g = .50 for fraternal twins. Substituting this value into the equation for siblings lets us write the correlation for dizygotic twins as

The last piece of information required for the twin method is to note that h² + e² = 1.0.

Hence, the twin method involves a series of three simultaneous equations in three unknowns. They are

R_mz = h² + he², (5.2.1)

R_dz = .5h² + he², (5.2.2)

and h² + e² = 1.0. (5.2.3)

An estimate of heritability may be derived in the following way. Subtract the equation for DZ twins from that for MZ twins,

Now multiply both sides by two,

Hence, we may obtain an estimate of the heritability by simply doubling the difference between the MZ and the DZ correlations,

Having obtained an estimate of heritability, the environmentability may now be estimated as simply 1.0 minus the heritability, or

Finally, just substitute the numeric values for h² and e² into the correlation for one of the twin types and solve for h. If we do this for the MZ twins, we have

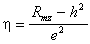so . (5.2.6)

Hence, equations (5.2.4), (5.2.5), and (5.2.6) may be used to solve for the path coefficients and for heritability and environmentability with the twin method.

To illustrate this, assume that the correlation for MZ pairs is .60 and the correlation for DZ pairs is .38. Then, using equation (5.2.4),

Solving for e2 using equation 5.2.5) gives

And substituting the numerical values into equation (5.2.6) gives the correlation between the environments of twins as

.

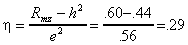For this trait 44% of the observed individual differences are attributable in some way to genetic individual differences, and the other 56% of phenotypic differences are attributable to the environment. The environments for siblings are correlated .29, signifying that something associated with being raised in the same family, having similar peers, living in the same neighborhood, etc. also contributes to twin similarity. The precise mechanism behind this correlation, of course, is open to speculation. The twin method can only give us a numerical estimate of the correlation.

5.3: Twins raised apart and adoptive siblings.

What happens when siblings are raised apart? In this case their environments will be uncorrelated so h = 0. The resulting correlation is

If these are full siblings, then g = .5. To obtain an estimate of h2 in this case, one would simply double the correlation for sibs raised apart.

A particularly important data point is when the sibs raised apart are identical twins, often denoted as MZA for monozygotic twins raised apart. In this case, g = 1 and the equation is

Hence, the correlation for identical twins raised apart provides a direct estimate of heritability.

Finally, it is possible to have genetically unrelated siblings raised in the same household. The two may be two adopted children, or quite often a single adoptee raised with the biological offspring of the adoptive parents. Here, g = 0, so the correlation becomes he2. This correlation provides a direct estimate of the extent to which environments make siblings similar.

5.0: Parent-offspring resemblance and the adoption design.

We have seen how genetic siblings raised in separate households can provide estimates of heritability. Such data, however, are relatively hard to gather. The most frequently encountered data of this type are for biological parents, often biological mothers, who give their children up for nonfamilial adoption. As we will see, the path models for parents and offspring in the adoption design turn out to be special cases of the path model for traditional nuclear families where the biological parents raise their own offspring. Hence, we start with the path model for parent-offspring resemblance in ordinary nuclear families, presented in Figure 3..

Figure 3. A path model for the resemblance between a parent and offspring in traditional nuclear families..

Gp = genotypic value for the parent 1; Ep = environmental value for the parent; Pp = phenotypic value for the parent. Go, Eo, and Po = genotypic, environmental and phenotypic values for the offspring.

Again, we find the familiar path coefficients h and e. Once again the quantity g is unknown. If there were simple additive allele action, and no assortative mating, then g = .50. Nonadditive variance will decrease g, while assortative mating will increase g. For the present exposition, we assume that g = .50. The quantity h is gone because that was the correlation between the environments of siblings. In this model for parents and offspring, it is assumed that the observable behavior of the parent influences the environment of the offspring. Hence, the path from P_p to E_o with coefficient t.

The predicted parent-ffspring correlation may be found using the rules for path analysis. The first way to traverse from Po to Pp begins with Po goes to Go (via path h), then to Gp (via g) and then to Pp (via h). The coefficients for this are h, .5, and h, giving .5h2. The second pathway is from Po to Eo (via e) to Pp. The pathways for this are t and e, giving the quantity te. Thus, the correlation between parent and offspring becomes

. (5.0.1)

One again, we see how similarity between parents and offspring confounds genetic with environmental transmission. If we only have an observed correlation (R_po), it is not possible to determine how much is due to shared genes (.5h²) and how much to shared environments (te).

The adoption design will also use the path diagram in Figure 3, but some path coefficients will be 0. For example, consider a biological parent who gives his/her child away for adoption. Because that parent does not raise the child, the path coefficient t = 0 in Figure 3. Hence, the correlation becomes

. (5.0.2)

Here, the subscript bpo is used to denote the biological parent-offspring correlation. We would simply multiply this correlation coefficient by 2 to obtain an estimate of h2.

An adoptive parent does not transmit genes to his/her adoptive offspring. Hence, the path between Gp and Go disappears. The resulting correlation for adoptive parent-offspring pairings becomes

. (5.0.3)

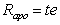
Again, the subscript apo is used to denote an adoptive parent-offspring pair. Note that the expected correlation for parents and offspring is the sum of the correlation between biological parent-offspring and adoptive parent-offspring.

Solving for the path coefficients in an adoption design requires at least two of the three correlations given aboveó(5.0.1), (5.0.2), and (5.0.3).. For example, suppose that a study collected data on a series of intact nuclear families and a number of adoptive families. Let the parent-offspring correlation be .32 and the adoptive parent-offspring correlation be .09. Then, we have the two simultaneous equations

and

Substituting .09 for te in the first equation gives

or

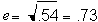
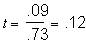Because e2 = 1 - h2, then e2 = 1 - .46 = .54. So, . Substituting this into the equation for adoptive parent offspring gives

.

6.0: Advanced Topics

The basics of quantitative analysis of human behavioral genetic data are outlined above. The requisite data are some correlations on twins, adoptees, etc. The requisite skills needed to perform a quantitative analysis are the path models (which have been given above) and some facility with solving simultaneous equations. There are, however, several advanced topics that merit discussion.

6.1: Pooling kinship correlations

In many behavioral genetic studies, data on the same phenotype are available from several different kinships. Such an example is given in Table X, adapted from the published data of Carey and Rice (1983) and Tellegen et al. (1989). The correlations in this case are from the Social Potency scale of the Multidimensional Personality Questionnaire. This scale is a measure of dominance, assertiveness, and leadership. There are four different twin types, identical and fraternal twins who have been raised together or apart. There are also data on adoptive parents and their offspring and on adoptive siblings, along with data on traditional nuclear families. The equations in Table X have only four unknownsóh, e, t, and h. However, there are eight different equations, meaning that there are many different ways of solving for these four unknown.

This type of situationówhen there are more observed data points (correlation in this case) than there are unknownsóis called an overdetermined system of linear equations. Far from being a disadvantage, these type of data are often sought out by behavioral geneticists because of their major advantageóthey can provide a statistical test for the path analysis model.

The actual statistical techniques required to perform this test are beyond the scope of this introduction, so the interested reader is referred to Neale and Cardon (199x) for more information. The philosophy behind the technique is to use all the data to obtain the best estimates of h, e, t, and h. These estimates will then be used to generate a series of predicted correlations for all the kinships in Table X. If these predicted correlations are fairly close to the observed correlations, then the path model is thought to be an adequate model. On the other hand, if the observed correlations are fairly different than their predicted values, then one rejects the path analysis model as being a good mathematical explanation for the data The search is then on for a more appropriate model to explain the data.

6.2: Genetic Mediation

Previously in this course, we learned that almost all behavioral traits have a moderate amount of heritability. The goal for behavioral genetics has shifted away from assessing and quantifying heritability and towards explaining the how of heritability. Path analysis used with data on relatives can be a very useful tool in this regard. Suppose that one was interested in the familial transmission of antisocial behavior. It is very unlikely that millenia of evolution have specifically shaped primate behavior for shoplifting, painting slogans on a wall, or taking a joy ride in a stolen car. Many ressearchers in this area hypothesize that the genetic influence on these types of behaviors is secondary to more primary psychological traits. Such traits might include personality variables, cognitive differences, motivational styles, etc., all of which combine to make it more likely that one person might engage in antisocial behavior while another, faced with the same situation, reacts with a prosocial alternative.

Figure 4. A path model for the resemblance of impulsivity and antisocial behavior in sib-pairs.

ASB = Antisocial Behavior; R1, R2 = residuals for sibs 1 and 2.

Figure 4 illustrates the approach. Here it is assumed that at least part of the reason for sibling resemblance for antisocial behavior (ASB in Figure 1) may be attributed to the personality trait of impulsivity. In addition to this personality trait, other factors may also make sibs similar for ASB. These are denoted by the residuals (the Rs) in Figure 1. Applying the rules of path analysis gives the following series of equations:

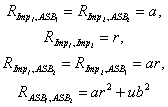
Once again, the use of advanced mathematical techniques permit the solution for the path coefficients. Hence one can obtain an estimate of a and assess to what extent the trait of impulsivity mediates the familial transmission of antisocial behavior.

6.3: Multivariate genetic analysis.

Thus far, we have discussed only one phenotype. It is also possible to use path analysis to examine two or more phenotypes in a single model. This is referred to as multivariate analysis.

A classic example of multivariate analysis has been the case of cognitive abilities. It has long been known that performance on verbal portions of cognitive tests (e.g., vocabulary, reading, word analogies) is correlated with performance on nonverbal tests (e.g., arithmetic, figure analogies, block design). It has also been demonstrated that there is heritability for both the verbal and nonverbal portions of these tests. But to what extent are the genes for verbal ability associated with the genes for nonverbal ability?

A momentís thought on the issue does not suggest an easy answer. It is possible that there might be no association. Perhaps, genes for individual differences in verbal ability influence neuroanatomical and neurophysiological structures in the brain specific to the processing of language, while very different loci operate in areas devoted to spatial perception and other nonverbal tasks. In this case, one might expect to find a very small genetic relationship between verbal and nonverbal ability. The two may be correlated mostly for environmental reasons such as differences in early experience and schooling.

On the other hand, there are strong interconnections between different areas of the brain and many different areas use the similar types of neurotransmitters, receptors, etc. Perhaps the same genes involving the synthesis, transport, release, etc. of a neurotransmitter that operates in both verbal and nonverbal areas. In such a case, one might expect some association between the genes that influence verbal performance and those for nonverbal skills.

Clearly, the only answer to these possibility is empirical. One must gather the appropriate data and obtain an empirical estimate of the genetic association between verbal and nonverbal talent. Although this sounds like a formidable task, the basic principles outlined above can be applied to this problem. Table 3 provides a hypothetical example.

Table 3. Hypothetical data giving the genotypic, environmental, and phenotypic values of individuals for both verbal and nonverbal ability.
	Verbal Ability			Nonverbal Ability
Observation	Gv	Ev	Pv	Gn	En	Pn
Abernathy Athabaska	113	96	107	101	108	106
Beulah Bottomwinger	92	74	77	103	113	104
.	.	.	.	.	.	.
Zelda Zakmeister	118	104	118	99	89	102

This table is almost identical to the Table 1, except that we now measure two different sets of genotypic, environmental, and phenotypic values, one set for verbal ability and the second set for nonverbal ability. Figure 4 presents a path diagram for these data.

Gv, Ev, Pv = genotypic, environmental, and phenotypic values for verbal ability; Gn, En, Pn = genotypic, environmental, and phenotypic values for nonverbal ability; hv, hn = square root of the heritabilities for verbal and nonverbal ability; ev, en = square root of the environmentabilites for verbal and nonverbal ability; rg = genetic correlation between the genotypic values for verbal and nonverbal abilities; re = environmental correlation between the environmental values for verbal and nonverbal abilities.

In a multivariate problem such as this, we subscript all the variables and the path coefficients h and e with either a v or an n to denote verbal and nonverbal ability, respectively. The only two new coefficients in Figure X are rg and re. The quantity rg is called the genetic correlation. Literally, it would be the correlation coefficient between the genotypic values for verbal ability in Table 1 and the genotypic values for nonverbal ability. The quantity re is termed the environmental correlation. It is the correlation between the environmental values for verbal and nonverbal ability.

Just as we cannot estimate heritability directly from genotypic values, we cannot directly estimate genetic and environmental correlations. They must be estimated indirectly using twin or adoption data. The relevant information in this case would be the correlation between verbal ability in twin 1 and nonverbal ability in twin 2. The mechanics of estimation and statistical testing are too advanced for this course. What is important, however, is the equation for the phenotypic values for verbal and nonverbal ability. Using the rules of path analysis, this correlation is

.

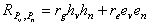In English, this equation says that the observed, phenotypic correlation between verbal and nonverbal ability is the sum of a genetic component (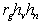) and an environmental component (). By performing the appropriate multivariate analysis, we will obtain estimates of both rg and re. In this way, we can assess the extent to which the genetic effects for verbal ability are associated (or not associated as the case may be) with those for nonverbal ability.

Problems:

In a study of a large number of twins raised together, the personality trait of neuroticism has an MZ correlation of .53 and a DZ correlation of .28.

a) calculate the heritability and the environmentability of this trait.

b) calculate the correlation between the environments of twins.

c) if someone gathered data on a series of identical twins raised apart, what would you predict the correlation to be?

d) if another researcher gathered data on unrelated siblings raised in the same families, what would you predict the correlation to be?

The MMPI Psychopathic-deviate scale was developed to be a predictor of juvenile delinquency and antisocial behavior. The correlation between biological mothers who gave their children up for adoption and their adopted children is .21.

a) estimate the heritability.

b) what would you predict to be the correlation for identical twins raised apart?

c) why is it not possible to predict the correlation for identical twins raised together using this estimate.

The National Merit twin sample gives representative estimates of twin correlations for cognitive abilities. For males the identical twin correlation was XXX and the fraternal twin correlation was XXX. For females, the respective correlations were XXX and XXX.

a) calculate the important path quantities for males.

b) calculate the important path quantities for females.

c) how well do you think these two sets of estimates agree?

In Denmark, an adoption study of criminality reported that the correlation between criminality in biological parents of adoptees and the adoptees was XXX. The correlation between the adoptive parents and the adoptees was XXX.

a) calculate the appropriate path quantities in this adoption study.

b) using these estimates, what would you predict the traditional parent-offspring correlation to be?

A similar study on twins in Denmark gave correlations of XXX for identical twins and XXX for fraternal twins.

a) calculate the appropriate path quantities for this twin study.

b) predict the correlation between biological parent and adoptees using this estimate.

Compare the estimates of heritability for the Danish adoptees in question XXX with those of the Danish twins in XXX. What reasons can you think of for the discrepancy?

Suppose that the heritability of a trait was .46, but nonadditive variance for a trait made g = .29 for siblings and DZ twins. If h = 0, then

a) calculate the expected MZ correlation.

b) calculate the expected DZ correlation.

c) using the two correlations calculated in a and b, re-estimate the quantities h², e² and h, but this time assuming that g = .50.

d) compare the estimates in c to their true values.