2 Model-fitting Results

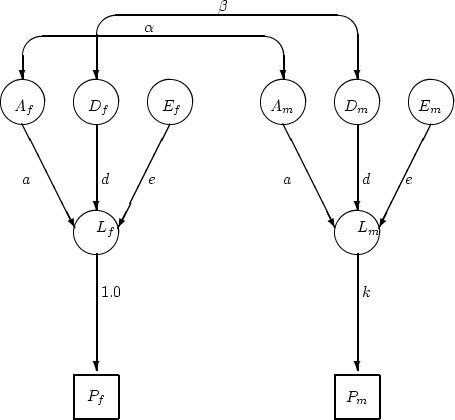
Table 9.4 shows the results of fitting several models: general G $\times$ E (I); full common-effects G $\times$ E (II); three common-effects sub-models (III-V); scalar G $\times$ E (VI); and no G $\times$ E interaction (VII). Parameter estimates subscripted $s$ and $m$ refer respectively to single (unexposed) and married twins. Models including genetic dominance parameters, rather than common environmental effects, were fitted to the data. The reader may wish to show that the overall conclusions concerning G $\times$ E interaction do not differ if shared environment parameters are substituted for genetic dominance.

Table 9.4: Parameter estimates obtained by fitting genotype $\times$ marriage interaction models to depression scores in Australian female twins.

	MODEL
Parameter	I	II	III	IV	V	VI	VII
$a_{s}$	0.187	0.187	0.207	0.209	0.186	0.206	0.188
$d_{s}$	0.106	0.105	-	-	-	-	-
$e_{s}$	0.240	0.240	0.246	0.245	0.257	0.247	0.246
$a_{m}$	0.048	0.048	0.163	0.162	0.186	0.206	0.188
$d_{m}$	0.171	0.173	-	-	-	-	-
$e_{m}$	0.232	0.232	0.243	0.245	0.232	0.247	0.246
$a'_{m}$	0.008	-	-	-	-	-	-
$k$	-	-	-	-	-	0.916	-
$\chi^{2}$	15.44	15.48	18.88	18.91	22.32	20.08	27.19
$d.f.$	11	12	14	15	15	15	16
	0.16	0.22	0.17	0.22	0.10	0.17	0.04
$AIC$	-6.56	-9.52	-9.12	-11.09	-7.68	-9.92	-4.81

Model I is a general G $\times$ E model with environment-specific additive genetic effects. It provides a reasonable fit to the data ( = 0.16), with all parameters of moderate size, except $a'_{m}$. Under model II, the parameter $a'_{m}$ is set to zero, and the fit is not significantly worse than model I ($\chi^{2}_{1}$ = 0.04, = 0.84). Thus, there is no evidence for environment-specific additive genetic effects. As an exercise, the reader may verify that the same conclusion can be made for environment-specific dominant genetic effects.

Under model III, we test whether the dominance effects on single and married individuals are significant. A $\chi^{2}$ difference of 3.40 ( = 0.183, 2 df.) between models III and II indicates that they are not. Consequently, model III, which excludes common dominance effects while retaining common additive genetic and specific environmental effects, is favored.

Models IV - VII are all sub-models of III: the first specifies no differences in environmental variance components across exposure groups; the second specifies no differences in genetic variance components across groups; the third constrains the genetic and environmental variance components of single twins to be scalar multiples of those of married twins; and the fourth specifies no genetic or environmental differences between the groups. When each of these is compared to model III using a $\chi^{2}$ difference test, only model VII (specifying complete homogeneity across groups) is significantly worse than the fuller model ($\chi^{2}_{2}$ = 8.28, p = 0.004). In order to select the best sub-models from IV, V and VI, Akaike's Information Criteria were used. These criteria indicate that model IV -- which allows for group differences in genetic, but not environmental, effects -- gives the most parsimonious explanation for the data. Under model IV, the heritability of depression is 42% for single, and 30% for married twins. This finding supports our hypothesis that marriage or marriage type relationships act as a buffer against the expression of inherited liability to depression.