2 Cholesky Decomposition

Clearly, we cannot resolve the genetic and environmental components of covariance without genetically informative data such as those from twins. Under our simple AE model we can write, for MZ and DZ pairs, the expected covariances between the multiple measures of first and second members very simply:

$$\begin{eqnarray*} {\bf C_{\mbox{MZ}}} & = & {\bf A} \\ {\bf C_{\mbox{DZ}}} & = & \alpha {\bf A} \end{eqnarray*}$$

with the total phenotypic covariance matrix being defined as in expression 10.4. The coefficient $\alpha$ in DZ twins is the familiar additive genetic correlation between siblings in randomly mating populations (i.e., 0.5).

The method of maximum likelihood, implemented in Mx, can be used to estimate A and E. However, there is an important restriction on the form of these matrices which follows from the fact that they are covariance matrices: they must be positive definite. It turns out that if we try to estimate A and E without imposing this constraint they will very often not be positive definite and thus give nonsense values (greater than or less than unity) for the genetic and environmental correlations. It is very simple to impose this constraint in Mx by recognizing that any positive definite matrix, F, can be decomposed into the product of a triangular matrix and its transpose:

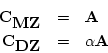$${\bf F} = {\bf TT}'\; ,$$ (65)

where T is a triangular matrix (i.e., one having fixed zeros in all elements above the diagonal). This is sometimes known as a triangular decomposition or a Cholesky factorization of F. Figure   shows this type of model as a path diagram for three variables. In our case, we represent the genetic and environmental covariance matrices in Mx by their respective Cholesky factorizations:

$${\bf A} = {\bf XX}'$$ (66)

and

$${\bf E} = {\bf ZZ}' \; ,$$ (67)

where X and Z are triangular matrices of additive genetic and within-family environment factor loadings.

A triangular matrix such as T, X, or Z is square, having the same number of rows and columns as there are variables. The first column has non-zero entries in every element; the second has a zero in the first element and free, non-zero elements everywhere else, and so on. Thus, the Cholesky factors of F, when F is a $3 \times 3$ matrix of the product ${\bf TT}'$, will have the form:

$${\bf T} = \left( \begin{array}{lll} b_{11} & 0 & 0\\ b_{21... ...{22} & 0 \\ b_{31} & b_{32} & b_{33} \end{array}\right) \; .$$

It is important to recognize that common factor models such as the one described in Section 10.3 are simply reduced Cholesky models with the first column of parameters estimated and all others fixed at zero.