


Next: 5 Common vs. Independent
Up: 4 Multiple Genetic Factor
Previous: 2 Cholesky Decomposition
Index
We illustrate the estimation of the genetic and environmental
covariance matrices for a simple case of skinfold measures
made on 11.5 year-old male twins from the
Medical College of Virginia Twin Study
(Schieken et al., 1989)![[*]](footnote.png) Our skinfold assessments include
four different measures which were obtained using standard
anthropometric techniques. The measures were obtained for biceps,
subscapular, suprailiac, and triceps skinfolds. The raw data were
averaged for the left and right sides and subjected to a logarithmic
transformation prior to analysis in order to remove the correlation
between error variance and skinfold measure. The
Our skinfold assessments include
four different measures which were obtained using standard
anthropometric techniques. The measures were obtained for biceps,
subscapular, suprailiac, and triceps skinfolds. The raw data were
averaged for the left and right sides and subjected to a logarithmic
transformation prior to analysis in order to remove the correlation
between error variance and skinfold measure. The 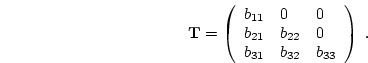 covariance matrices for the male MZ and DZ twins are given in
Table 10.3.
covariance matrices for the male MZ and DZ twins are given in
Table 10.3.
Table 10.3:
Covariance matrices for skinfold measures in MZ and DZ
male twins.
| |
Dizygotic Male Pairs (N=33)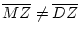 |
| |
BIC1 |
SSC1 |
SUP1 |
TRI1 |
BIC2 |
SSC2 |
SUP2 |
TRI2 |
| BIC1 |
.1538 |
|
|
|
|
|
|
|
| SSC1 |
.1999 |
.3007 |
|
|
|
|
|
|
| SUP1 |
.2266 |
.3298 |
.3795 |
|
|
|
|
|
| TRI1 |
.1285 |
.1739 |
.2007 |
.1271 |
|
|
|
|
| BIC2 |
.0435 |
.0336 |
.0354 |
.0376 |
.1782 |
|
|
|
| SSC2 |
.0646 |
.0817 |
.0741 |
.0543 |
.2095 |
.3081 |
|
|
| SUP2 |
.0812 |
.0901 |
.0972 |
.0666 |
.2334 |
.3241 |
.3899 |
|
| TRI2 |
.0431 |
.0388 |
.0376 |
.0373 |
.1437 |
.1842 |
.2108 |
.1415 |
| |
Monozygotic Male Pairs (N=84)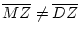 |
| |
BIC1 |
SSC1 |
SUP1 |
TRI1 |
BIC2 |
SSC2 |
SUP2 |
TRI2 |
| BIC1 |
.1285 |
|
|
|
|
|
|
|
| SSC1 |
.1270 |
.1759 |
|
|
|
|
|
|
| SUP1 |
.1704 |
.2156 |
.3031 |
|
|
|
|
|
| TRI1 |
.1035 |
.1101 |
.1469 |
.1041 |
|
|
|
|
| BIC2 |
.0982 |
.1069 |
.1491 |
.0824 |
.1233 |
|
|
|
| SSC2 |
.0999 |
.1411 |
.1848 |
.0880 |
.1295 |
.1894 |
|
|
| SUP2 |
.1256 |
.1654 |
.2417 |
.1095 |
.1616 |
.2185 |
.2842 |
|
| TRI2 |
.0836 |
.0907 |
.1341 |
.0836 |
.1010 |
.1134 |
.1436 |
.1068 |
| Variable Labels: BIC=Biceps;
SSC=Subscapular; SUP=Suprailiac; |
| TRI=Triceps. ``1'' and ``2'' refer to measures
on first and second twins |
An example Mx program for estimating the Cholesky factors of the
additive genetic and within-family environmental covariance matrices
is given in Appendix ![[*]](crossref.png) . The matrices X and Z are now declared as free lower triangular matrices.
. The matrices X and Z are now declared as free lower triangular matrices.
When this program is run with the data from male twins, we obtain a
goodness-of-fit chi-squared of 68.92 for 52 d.f. (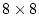 )
suggesting that the AE model gives a reasonable fit to these data.
Setting the off-diagonal elements of the genetic factors to zero
yields a chi-squared that may be compared using the difference test to
see whether the measures can be regarded as genetically independent.
This chi-squared turns out to be 110.96 for 6 d.f. which is highly
significant. Therefore, the genetic correlations between these
skinfold measures cannot be ignored. Similarly, setting the
environmental covariances to zero yields a significant increase in
chi-squared of 356.98, also for 6 d.f. Clearly, there are also highly
significant environmental covariances among the four variables.
)
suggesting that the AE model gives a reasonable fit to these data.
Setting the off-diagonal elements of the genetic factors to zero
yields a chi-squared that may be compared using the difference test to
see whether the measures can be regarded as genetically independent.
This chi-squared turns out to be 110.96 for 6 d.f. which is highly
significant. Therefore, the genetic correlations between these
skinfold measures cannot be ignored. Similarly, setting the
environmental covariances to zero yields a significant increase in
chi-squared of 356.98, also for 6 d.f. Clearly, there are also highly
significant environmental covariances among the four variables.
Table 10.4 gives the estimates of the Cholesky factors of
the genetic and environmental covariance matrices produced by Mx.
Table 10.4:
Mx estimates of the cholesky factors in the genetic and
environmental covariance matrices.
| |
Genetic Factor |
|
Environmental Factor |
| Variable |
1 |
2 |
3 |
4 |
|
1 |
2 |
3 |
4 |
| Biceps |
0.340 |
0.000 |
0.000 |
0.000 |
|
0.170 |
0.000 |
0.000 |
0.000 |
| Subscapular |
0.396 |
0.182 |
0.000 |
0.000 |
|
0.160 |
0.138 |
0.000 |
0.000 |
| Suprailiac |
0.487 |
0.159 |
0.148 |
0.000 |
|
0.180 |
0.117 |
0.093 |
0.000 |
| Triceps |
0.288 |
0.016 |
0.036 |
0.110 |
|
0.117 |
0.039 |
-0.004 |
0.085 |
Carrying out the pre- and post-multiplication of the Cholesky factors
(see equations 10.8 and 10.9) gives the
maximum-likelihood estimates of the genetic and environmental
covariance matrices, which we present in the upper part of
Table 10.5. The lower part of Table 10.5 gives the
matrices of genetic and environmental correlations derived from these
covariances (see 10.5 and 10.6).
Table 10.5:
Maximum-likelihood estimates of genetic and environmental
covariance (above the diagnoals) and correlation (below the
diagonals) matrices for skinfold measures.
| |
Genetic |
|
Environmental |
| Variable |
BIC |
SSC |
SUP |
TRI |
|
BIC |
SSC |
SUP |
TRI |
| Biceps |
0.116 |
0.135 |
0.166 |
0.098 |
|
0.029 |
0.027 |
0.030 |
0.020 |
| Subscapular |
0.909 |
0.190 |
0.222 |
0.117 |
|
0.759 |
0.044 |
0.045 |
0.024 |
| Suprailiac |
0.914 |
0.955 |
0.284 |
0.148 |
|
0.769 |
0.908 |
0.054 |
0.025 |
| Triceps |
0.927 |
0.863 |
0.894 |
0.097 |
|
0.778 |
0.757 |
0.716 |
0.023 |
| Note: The variances are given on the
diagonals of the two matrices; |
We see that the genetic correlations between the four skin-fold
measures are indeed very large, suggesting that the amount of fat at
different sites of the body is almost entirely under the control of the same
genetic factors. However, in this example, the environmental
correlations also are quite large, suggesting that environmental factors
which affect the amount of fat at one site also have a generalized
effect over all sites.



Next: 5 Common vs. Independent
Up: 4 Multiple Genetic Factor
Previous: 2 Cholesky Decomposition
Index
Jeff Lessem
2000-03-20
![[*]](footnote.png) Our skinfold assessments include
four different measures which were obtained using standard
anthropometric techniques. The measures were obtained for biceps,
subscapular, suprailiac, and triceps skinfolds. The raw data were
averaged for the left and right sides and subjected to a logarithmic
transformation prior to analysis in order to remove the correlation
between error variance and skinfold measure. The
Our skinfold assessments include
four different measures which were obtained using standard
anthropometric techniques. The measures were obtained for biceps,
subscapular, suprailiac, and triceps skinfolds. The raw data were
averaged for the left and right sides and subjected to a logarithmic
transformation prior to analysis in order to remove the correlation
between error variance and skinfold measure. The 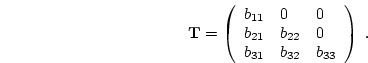 covariance matrices for the male MZ and DZ twins are given in
Table 10.3.
covariance matrices for the male MZ and DZ twins are given in
Table 10.3.
![[*]](crossref.png)