1 Path Coefficients Model: Example of Standardized Tracing Rules

When applying the tracing rules, it helps to draw out each tracing route to ensure that they are neither forgotten nor traced twice. In the traditional path model of Figure 5.4a, to derive the expected twin covariance for the case of monozygotic twin pairs reared together, we can trace the following routes:

$$\begin{eqnarray*} \mbox{(i)} & & P1 \stackrel{c}{\longleftarrow } C1 \stackrel{1... ...el{1}{\longleftrightarrow } D2 \stackrel{d}{\longrightarrow } P2 \end{eqnarray*}$$

so that the expected covariance between MZ twin pairs reared together will be

$$r_{MZ} = c^2 + a^2 + d^2 .$$ (30)

In the case of dizygotic twin pairs reared together, we can trace the following routes:

$$\begin{eqnarray*} \mbox{(i)} & & P1 \stackrel{c}{\longleftarrow } C1 \stackrel{1... ...el{1}{\longleftrightarrow } D2 \stackrel{d}{\longrightarrow } P2 \end{eqnarray*}$$

yielding an expected covariance between DZ twin pairs of

$$r_{DZ} = c^2 + 0.5 a^2 + 0.25 d^2 .$$ (31)

The expected variance of a variable -- again assuming we are working with standardized variables -- is derived by tracing all possible routes from the variable back to itself, without violating any of the tracing rules given in Section 5.4.1 above. Thus, following paths from P1 to itself we have

$$\begin{eqnarray*} \mbox{(i)} & & P1 \stackrel{e}{\longleftarrow } E1 \stackrel{e... ...tackrel{d}{\longleftarrow } D1 \stackrel{d}{\longrightarrow } P1 \end{eqnarray*}$$

yielding the predicted variance for 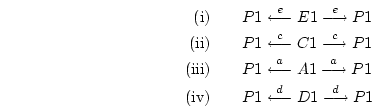$P1$ or $P2$ in Figure 5.4a of

$$V_P = e^2 + c^2 + a^2 + d^2 .$$ (32)

An important assumption implicit in Figure 5.4 is that an individual's additive genetic deviation is uncorrelated with his or her shared environmental deviation (i.e., there are no arrows connecting the latent $C$ and $A$ variables of an individual). In Chapter  we shall discuss how this assumption can be relaxed. Also implicit in the coefficient of 0.5 for the covariance of the additive genetic values of DZ twins or siblings is the assumption of random mating, which we shall also relax in Chapter .