2 Variance Components Model: Example of Unstandardized Tracing Rules

Following the unstandardized tracing rules, the expected covariances of twin pairs in the variance components model of Figure 5.4b, are also easily derived. For the case of monozygotic twin pairs reared together (MZT), we can trace the following routes:

$$\begin{eqnarray*} \mbox{(i)} & & P1 \stackrel{1}{\longleftarrow } C1 \stackrel{V... ...{V_D}{\longleftrightarrow } D2 \stackrel{1}{\longrightarrow } P2 \end{eqnarray*}$$

so that the expected covariance between MZ twin pairs reared together will be

$$\mbox{Cov}(MZT) = V_C + V_A + V_D .$$

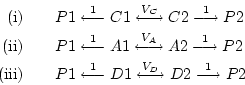
Only the latter two chains contribute to the expected covariance of MZ twin pairs reared apart, as they do not share their environment. The expected covariance of MZ twin pairs reared apart (MZA)is thus

$$\mbox{Cov}(MZA) = V_A + V_D .$$

In the case of dizygotic twin pairs reared together (DZT), we can trace the following routes:

$$\begin{eqnarray*} \mbox{(i)} & & P1 \stackrel{1}{\longleftarrow } C1 \stackrel{V... ...{V_D}{\longleftrightarrow } D2 \stackrel{1}{\longrightarrow } P2 \end{eqnarray*}$$

yielding an expected covariance between DZ twin reared together of

$$\mbox{Cov}(DZT) = V_C + 0.5 V_A + 0.25 V_D.$$

Similarly, the expected covariance of DZ twin pairs reared apart (DZA)is

$$\mbox{Cov}(DZA) = 0.5 V_A + 0.25 V_D.$$

In deriving expected variances of unstandardized variables, any chain from a dependent variable to an independent variable will include the double-headed arrow from the independent variable to itself (unless it also includes a double-headed arrow connecting that variable to another independent variable) and each path from an dependent variable to an independent variable and back to itself is only counted once. In this example the expected phenotypic variance, for all groups of relatives, is easily derived by tracing all the paths from 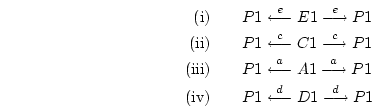$P1$ to itself:

$$\begin{eqnarray*} \mbox{(i)} & & P1 \stackrel{1}{\longleftarrow } E1 \stackrel{... ...{V_D}{\longleftrightarrow } D1 \stackrel{1}{\longrightarrow } P1 \end{eqnarray*}$$

yielding the predicted variance for P1 or P2 in Figure 5.4b of

$$V_P = V_E + V_C + V_A + V_D.$$

The equivalence between Figures 5.4a and 5.4b comes from the biometrical principles outlined in Chapter 3: $a^2$, $c^2$, $e^2$, and $d^2$ are defined as $\frac{V_A}{V_P}$, $\frac{V_C}{V_P}$, $\frac{V_E}{V_P}$, and $\frac{V_D}{V_P}$, respectively. Since correlations are calculated as covariances divided by the product of the square roots of the variances (see Chapter 2), the twin correlations in Figure 5.4a may be derived using the covariances and variances in Figure 5.4b. Thus, in Figure 5.4b, the correlation for MZ pairs reared together is

$$\begin{eqnarray*}r_{\mbox{MZT}} & = & \frac{V_C + V_A + V_D} {\sqrt{(V_C + V_A +... ...P} + \frac{V_A}{V_P} + \frac{V_D}{V_P}\\ & = & c^2 + a^2 + d^2 \end{eqnarray*}$$

Similarly, the correlations for MZ twins reared apart, and for DZ twins together and apart are

$$\begin{eqnarray*}r_{\mbox{MZA}} & = & a^2 + d^2 \\ r_{\mbox{DZT}} & = & c^2 + 0.5a^2 + 0.25d^2 \\ r_{\mbox{DZA}} & = & 0.5a^2 + 0.25d^2 , \end{eqnarray*}$$

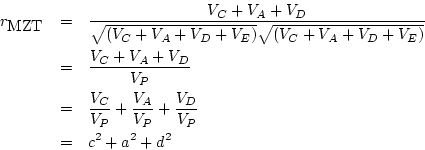
as in the case of Figure 5.4a.