2 Body Mass Index in Twins

Table 6.1 summarizes twin correlations and other summary statistics (see Chapter 2) for untransformed BMI, defined as weight (in kilograms) divided by the square of height (in meters). BMI is an index of obesity which has been widely used in epidemiologic research (Bray, 1976; Jeffrey and Knauss, 1981), and has recently been the subject of a number of genetic studies [Grilo and Pogue-Guile, 1991,Cardon and Fulker, 1992,Stunkard et al., 1986]. Values between 20-25 are considered to fall in the normal range for this population, with BMI 20 taken to indicate underweight, BMI $>$ 25 overweight, and BMI $>$ 28 obesity (Australian Bureau of Statistics, 1977) though standards vary across nations. The data analyzed here come from a mailed questionnaire survey of volunteer twin pairs from the Australian NH&MRC twin register conducted in 1981 [Martin and Jardine, 1986,Jardine, 1985]. Questionnaires were mailed to 5967 pairs age 18 years and over, with completed questionnaires returned by both members of 3808 (64%) pairs, and by one twin only from approximately 550 pairs, yielding an individual response rate of 68%.

Table 6.1: Twin correlations and summary statistics for untransformed BMI in twins concordant for participation in the Australian survey. BMI is calculated as $kg/m^2$. Notation used is $N$: sample size in pairs; $r$: correlation; $\bar{x}$: mean; $\sigma^2$: variance; skew: skewness; kurt: kurtosis. Groups consist of monozygotic (MZ) or dizygotic (DZ) twin pairs who are male (M) female (F) or opposite-sex (OS).

			First Twin$^\dagger$				Second Twin
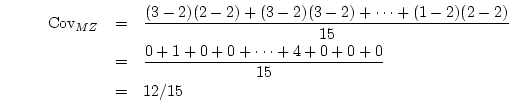	$N$	$r$	$\bar{x}$	$\sigma^2$	skew	kurt	$\bar{x}$	$\sigma^2$	skew	kurt
MZF
Young	534	.78	21.25	7.73	1.82	6.84	21.30	8.81	2.14	9.44
Older	637	.69	23.11	11.87	1.22	2.53	22.97	11.25	1.08	2.11
DZF
Young	328	.30	21.58	8.56	1.75	6.04	21.64	9.84	2.38	12.23
Older	380	.32	22.77	10.93	1.40	4.03	22.95	12.63	1.26	2.43
MZM
Young	251	.77	22.09	5.95	0.28	0.10	22.13	5.77	0.40	0.30
Older	281	.70	24.22	6.42	0.11	-0.05	24.30	7.85	0.43	0.63
DZM
Young	184	.32	22.71	8.16	1.00	1.71	22.61	9.63	1.55	6.24
Older	137	.37	24.18	8.28	0.41	0.70	24.08	7.42	0.72	0.43
DZOS
Young	464	.23	21.33	6.89	1.06	1.84	22.47	6.81	0.76	1.72
Older	373	.24	23.07	12.63	1.23	2.24	24.65	8.52	0.88	1.49
$\dagger$ Female twins are `first twin' in opposite-sex pairs.

The total sample has been subdivided into a young cohort, aged 18-30 years, and an older cohort aged 31 and above. This allows us to examine the consistency of evidence for environmental or genetic determination of BMI from early adulthood to maturity. For each cohort, twin pairs have been subdivided into five groups: monozygotic female pairs (MZF), monozygotic male pairs (MZM), dizygotic female pairs (DZF), dizygotic male pairs (DZM) and opposite-sex pairs (DZFM). We have avoided pooling MZ or like-sex DZ twin data across sex before computing summary statistics. Pooling across sexes is inappropriate unless it is known that there is no gender difference in mean, variance, or twin pair covariance, and no genotype $\times$ sex interaction; it should almost always be avoided. Among same-sex pairs, twins were assigned as first or second members of a pair at random. In the case of opposite-sex twin pairs, data were ordered so that the female is always the first member of the pair.

In both sexes and both cohorts, MZ twin correlations are substantially higher than like-sex DZ correlations, suggesting that there may be a substantial genetic contribution to variation in BMI. In the young cohort, the like-sex DZ correlations are somewhat lower than one-half of the corresponding MZ correlations, but this finding does not hold up in the older cohort. In terms of additive genetic ($V_A$) and dominance genetic ($V_D$) variance components, the expected correlations between MZ and DZ pairs are respectively $r_{MZ} = \mbox{$V_A$} + \mbox{$V_D$}$ and $r_{DZ} = 0.5 \mbox{$V_A$} + 0.25 \mbox{$V_D$}$, respectively (see Chapters 3 and ). Thus the fact that the like-sex DZ twin correlations are less than one-half the size of the MZ correlations in the young cohort suggests a contribution of genetic dominance, as well as additive genetic variance, to individual differences in BMI. Model-fitting analyses (e.g., [] are needed to determine whether the data:

1. Are consistent with simple additive genetic effects
2. Provide evidence for significant dominance genetic effects
3. Enable us to reject a purely environmental model
4. Indicate significant genotype $\times$ age-cohort interaction.

Skewness and kurtosis measures in Table 6.1 indicate substantial non-normality of the marginal distributions for raw BMI. We have also computed the polynomial regression of absolute intra-pair difference in BMI values on pair sumseparately for each like-sex twin group. These are summarized in Table 6.2. If the joint distribution of twin pairs for BMI is bivariate normal, these regressions should be non-significant. Here, however, we observe a highly significant regression: on average, pairs with high BMI values also exhibit larger intra-pair differences in BMI. This is likely to be an artefact of scale, since using a log-transformation substantially reduces the magnitude of the polynomial regression (as well as reducing marginal measures of skewness and kurtosis).

Table 6.2: Polynomial regression of absolute intra-pair difference in BMI ($\vert$BMI$_{T1} -$BMI$_{T2}\vert$) on pair sum (BMI$_{T1}$ + BMI$_{T2}$), sum$^2$, and sum$^3$. The multiple regression on these three quantities is shown for raw and log-transformed BMI scores.

	Raw BMI	Log BMI
Sample	R$^2$	R$^2$
Young MZF	0.11***	0.04***
Older MZF	0.16***	0.06***
Young MZM	0.10***	0.04*
Older MZM	0.09***	0.03*
Young DZF	0.34***	0.15***
Older DZF	0.27***	0.12***
Young DZM	0.15***	0.06*
Older DZM	0.03	0.01
***$p<.001$; *$p<.05$.

In general, raw data or variance-covariance matrices, not correlations, should be used for model-fitting analyses with continuously distributed variables such as BMI. The simple genetic models we fit here predict no difference in variance between like-sex MZ and DZ twin pairs, but the presence of such variance differences may indicate that the assumptions of the genetic model are violated. This is an important point which we must consider in some detail. To many researchers the opportunity to expose an assumption as false may seem like something to be avoided if possible, because it may mean i) more work or b) difficulty publishing the results. But there are better reasons not to use a technique that hides assumption failure? For sure, if we fitted models to correlation matrices, variance differences would never be observed, but to do so would be like, in physics, breaking the thermometer if a temperature difference did not agree with the theory. Rather, we should look at failures of assumptions as opportunities in disguise. First, a novel effect may have been discovered! Second, if the effect biases the parameters of intereset, it may be possible to contol for the effect statistically, and therefore obtain unbiased estimates. Third, we may have the opportunity to develop a new and useful method of analysis.

To return to the task in hand, we present summary twin pair covariance matrices in Table 6.3.

Table 6.3: Covariances of Twin Pairs for Body Mass Index: 1981 Australian Survey. BMI = $7\times \ln (\mbox{kg}/(\mbox{m}^2))$.

Young Cohort ($<30$)
	Covariance Matrix		Means$^a$
	Twin 1	Twin 2	$\bar{x}^\prime$
MZ female pairs	(N=534 pairs)
Twin 1	0.7247	0.5891	0.3408
Twin 2	0.5891	0.7915	0.3510
DZ female pairs	(N=328 pairs)
Twin 1	0.7786	0.2461	0.4444
Twin 2	0.2461	0.8365	0.4587
MZ male pairs	(N=251 pairs)
Twin 1	0.5971	0.4475	0.6248
Twin 2	0.4475	0.5692	0.6378
DZ male pairs	(N=184 pairs)
Twin 1	0.7191	0.2447	0.8079
Twin 2	0.2447	0.8179	0.7690
Opposite-sex pairs	(N=464 pairs)
Female twin	0.6830	0.1533	0.3716
Male twin	0.1533	0.6631	0.7402
Older Cohort ($\geq 30$)
	Covariance Matrix		Means$^a$
	Twin	1 Twin 2	$\bar{x}^\prime$
MZ female pairs	(N=637 pairs)
Twin 1	0.9759	0.6656	0.9087
Twin 2	0.6656	0.9544	0.8685
DZ female pairs	(N=380 pairs)
Twin 1	0.9150	0.3124	0.8102
Twin 2	0.3124	1.0420	0.8576
MZ male pairs	(N=281 pairs)
Twin 1	0.5445	0.4128	1.2707
Twin 2	0.4128	0.6431	1.2884
DZ male pairs	(N=137 pairs)
Twin 1	0.6885	0.2378	1.2502
Twin 2	0.2378	0.5967	1.2281
Opposite-sex pairs	(N=373 pairs)
Female twin	1.0363	0.1955	0.8922
Male twin	0.1955	0.6463	1.3860
$^a\bar{x}^\prime=\bar{x}-21$.

These statistics have been computed for 7 ln (BMI), and means have been computed as ( $7 \mbox{ln (BMI)} - 21$), to yield summary statistics with magnitudes of approximately unity. Rescaling the data in this way will often improve the efficiency of the optimization routines used in model-fitting analyses [Gill et al., 1981]