



Next: 3 Steps in Power
Up: 7 Power and Sample
Previous: 1 Introduction
Index
2 Factors Contributing to Power
One of the greatest advantages of the model-fitting approach is that
it allows us to conduct tests of significance
of alternative hypotheses. We can ask, for example, whether a given
data set really supports our assertion that shared environmental
effects contribute to variation in one trait or another (i.e., is 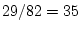 ?).
Our ability to show that a specific effect is important obviously
depends on a number of factors. These include:
?).
Our ability to show that a specific effect is important obviously
depends on a number of factors. These include:
- The effect under consideration, for example,
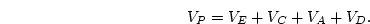 or
or 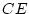 ;
;
- The actual size of the effect in the population being studied
-- larger values are detected more easily than small values;
- The probability level adopted as the conventional criterion for
rejection of the null-hypothesis that the effect is zero --
rejection at higher significance levels will be less likely to occur
for a given size of effect;
- The actual size of the sample chosen for study -- larger
samples can detect smaller effects;
- The actual composition of the sample with respect to the
relative frequencies of the different biological and social
relationships selected for study;
- The level of measurement used -- categorical, ordinal, or
continuous.
All of these considerations lead us to the important question of
power. If we are trying to get a sense of what we are likely to be
able to infer from our own data set, or if we are considering a new
study, we must ask either ``What inferences can we hope to be able to
make with our data set?" or ``What kind of data set and sample sizes
is it likely we will need to answer a particular set of questions?"
In the next section we show how to answer these questions in relation
to simple hypotheses with twin studies and suggest briefly how these
issues may be explored for more complex designs and hypotheses.




Next: 3 Steps in Power
Up: 7 Power and Sample
Previous: 1 Introduction
Index
Jeff Lessem
2002-03-21