



Next: 4 Power for the
Up: 7 Power and Sample
Previous: 2 Factors Contributing to
Index
3 Steps in Power Analysis
The basic approach to power analysis is to imagine that we are doing
an identical study many times. For example, we pretend that we are
trying to estimate 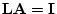 , and
, and 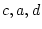 for a given population by taking
samples of a given number of MZ and DZ twins. Each sample would give
somewhat different estimates of the parameters, depending on how many
twins we study, and how big
for a given population by taking
samples of a given number of MZ and DZ twins. Each sample would give
somewhat different estimates of the parameters, depending on how many
twins we study, and how big 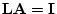 , and
, and 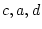 are in the study
population. Suppose we did a very large number of studies and
tabulated all the estimates of the shared environmental component,
are in the study
population. Suppose we did a very large number of studies and
tabulated all the estimates of the shared environmental component,
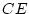 . In some of the studies, even though there was some shared
environment in the population, we would find estimates of
. In some of the studies, even though there was some shared
environment in the population, we would find estimates of 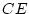 that
were not significant. In these cases we would commit ``type II
errors.'' That is, we would not find a
significant effect of the shared environment even though the value of
that
were not significant. In these cases we would commit ``type II
errors.'' That is, we would not find a
significant effect of the shared environment even though the value of
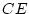 in the population was truly greater than zero. Assuming we were
using a
in the population was truly greater than zero. Assuming we were
using a  test for 1 df to test the significance of the
shared environment, and we had decided to use the conventional 5%
significance level, the probability of Type II error would be the
expected proportion of samples in which we mistakenly decided in favor
of the null hypothesis that
test for 1 df to test the significance of the
shared environment, and we had decided to use the conventional 5%
significance level, the probability of Type II error would be the
expected proportion of samples in which we mistakenly decided in favor
of the null hypothesis that 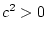 . These cases would be those in
which the observed value of
. These cases would be those in
which the observed value of  was less than 3.84, the 5%
critical value for 1 df. The other samples in which
was less than 3.84, the 5%
critical value for 1 df. The other samples in which  was
greater than 3.84 are those in which we would decide, correctly, that
there was a significant shared environmental effect in the population.
The expected proportion of samples in which we decide correctly
against the null hypothesis is the power of the test.
Designing a genetic study boils down to deciding on the numbers and
types of relationships needed to achieve a given power for the test of
potentially important genetic and environmental factors. There is no
general solution to the problem of power. The answers will depend on
the specific values we contemplate for all the factors listed above.
Before doing any power study, therefore, we have to decide the
following questions in each specific case:
was
greater than 3.84 are those in which we would decide, correctly, that
there was a significant shared environmental effect in the population.
The expected proportion of samples in which we decide correctly
against the null hypothesis is the power of the test.
Designing a genetic study boils down to deciding on the numbers and
types of relationships needed to achieve a given power for the test of
potentially important genetic and environmental factors. There is no
general solution to the problem of power. The answers will depend on
the specific values we contemplate for all the factors listed above.
Before doing any power study, therefore, we have to decide the
following questions in each specific case:
- What kinds of relationships are to be considered?
- What significance level is to be used in hypothesis testing?
- What values are we assuming for the various effects of interest
in the population being studied?
- What power do we want to strive for in designing the study?
When we have answered these questions exactly, then we can conduct a
power analysis for the specified set of conditions by following some
basic steps:
- Obtain expected covariance matrices for each set of
relationships by substituting the assumed values of the population
parameters in the model for each relationship.
- Assign some initial arbitrary sample sizes to each separate
group of relatives.
- Use Mx to analyze the expected covariance matrices just as
we would to analyze real data and obtain the
 value for
testing the specific hypothesis of interest.
value for
testing the specific hypothesis of interest.
- Find out (from statistical tables) how big that
 has to
be to guarantee the power we need.
has to
be to guarantee the power we need.
- Use a simple formula (given below) to multiply our assumed
sample size and solve for the sample size we need.
It is essential to remember that the sample size we obtain in step
five only applies to the particular effect, design, sample sizes, and
even to the distribution of sample sizes among the different types of
relationship assumed in a specific power calculation. To explore the
question of power fully, it often will be necessary to consider a
number, sometimes a large number, of different designs and population
values for the relevant effects of genes and environment.




Next: 4 Power for the
Up: 7 Power and Sample
Previous: 2 Factors Contributing to
Index
Jeff Lessem
2002-03-21