



Next: 2 Cholesky Decomposition
Up: 4 Multiple Genetic Factor
Previous: 4 Multiple Genetic Factor
Index
1 Genetic and Environmental Correlations
We now turn from the one- and two-factor multivariate genetic models
described above and consider more general multivariate formulations which
may encompass many genetic and environmental factors. These more general
approaches subsume the simpler techniques described above.
Consider a simple extension of the one- and two-factor AE models for
multiple variables (sections 10.3.2-10.3.4). The total
phenotypic covariance matrix in a population, 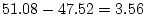 , can be
decomposed into an additive genetic component, A, and a random
environmental component, E:
, can be
decomposed into an additive genetic component, A, and a random
environmental component, E:
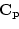 |
(62) |
We are leaving out the shared environment in this example just for
simplicity. More complex expectations for 10.4 may be written
without affecting the basic idea. ``A'' is called the
additive genetic covariance matrix and ``E'' the random
environmental covariance matrix. If A is diagonal, then the
traits comprising A are genetically independent; that is, there
is no ``additive genetic covariance'' between them. One
interpretation of this is that different genes affect each of the
traits. Similarly, if the environmental covariance matrix, E,
is diagonal, we would conclude that each trait is affected by quite
different environmental factors.
On the other hand, suppose A were to have significant off-diagonal
elements. What would that mean? Although there are many reasons why this
might happen, one possibility is that at least some genes are having
effects on more than one variable. This is known as pleiotropy
in the classical genetic literature (see
Chapter 3). Similarly, significant off-diagonal elements in
E (or C, if it were included in the model) would indicate that
some environmental factors influence more than one trait at a time.
The extent to which the same genes or environmental factors contribute to
the observed phenotypic correlation between two variables is often
measured by the genetic or environmental correlation
between the
variables. If we have estimates of the genetic and environmental
covariance matrices, A and E, the genetic correlation ( )
between variables
)
between variables 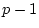 and
and 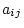 is
is
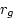 |
(63) |
and the environmental correlation, similarly, is
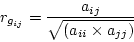 |
(64) |
The analogy with the familiar formula for the correlation coefficient is
clear. The genetic covariance between two phenotypes is quite distinct
from the genetic correlation. It is possible for two traits to have a
very high genetic correlation yet have little genetic covariance. Low
genetic covariance could arise if either trait had low genetic variance.
Vogler (1982) and Carey (1988) discuss these issues in greater depth.




Next: 2 Cholesky Decomposition
Up: 4 Multiple Genetic Factor
Previous: 4 Multiple Genetic Factor
Index
Jeff Lessem
2002-03-21