



Next: 2 Unary Operations
Up: 1 Binary Operations
Previous: 1 Addition and subtraction
Index
2 Matrix multiplication
Matrices are conformable for
multiplication if and only if the number of columns in the first
matrix equals the number of rows in the second matrix. This means
that adjacent columns and rows must be of the same order. For
example, the matrix product

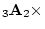 may be calculated; the result is a
may be calculated; the result is a 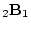 matrix. In general,
if we multiply two matrices
matrix. In general,
if we multiply two matrices
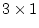
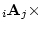 , the result will be of order
, the result will be of order 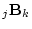 .
Matrix multiplication involves calculating a sum of cross
products among rows of the first matrix and columns of
the second matrix in all possible combinations.
.
Matrix multiplication involves calculating a sum of cross
products among rows of the first matrix and columns of
the second matrix in all possible combinations.
This is written
The only exception to the above rule is multiplication by a
single number called a scalar. Thus, for example,
by convention this is often written as
Although convenient and often found in the literature, we do not
recommend this style of matrix formulation, but prefer use of the
kronecker product. The kronecker product of two matrices, symbolized
 is formed by multiplying each element of A
by the matrix B. If A is a scalar, every element of the
matrix B is multiplied by the scalar.
The simplest example of matrix multiplication is to multiply a vector
by itself. If we premultiply a column vector (
is formed by multiplying each element of A
by the matrix B. If A is a scalar, every element of the
matrix B is multiplied by the scalar.
The simplest example of matrix multiplication is to multiply a vector
by itself. If we premultiply a column vector (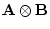 ) by its
transpose
) by its
transpose![[*]](footnote.png) ,
the result is a scalar called the inner
product. For example, if
,
the result is a scalar called the inner
product. For example, if
then the inner product is
which is the sum of the squares of the elements of the vector 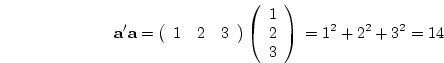 .
This has a simple graphical representation when
.
This has a simple graphical representation when 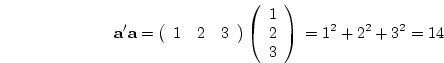 is of
dimension
is of
dimension 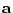 (see Figure 4.1).
(see Figure 4.1).
Figure 4.1:
Graphical
representation of the inner product 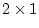 of a
of a 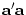 vector
vector 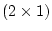 ,
with
,
with
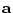 . By Pythagoras' theorem, the distance of the point
. By Pythagoras' theorem, the distance of the point 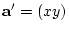 from the origin
from the origin 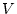 is
is
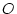 , which is the square root of
the inner product of the vector.
, which is the square root of
the inner product of the vector.
 |




Next: 2 Unary Operations
Up: 1 Binary Operations
Previous: 1 Addition and subtraction
Index
Jeff Lessem
2002-03-21
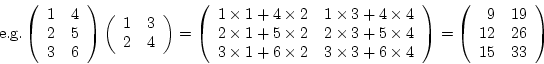

![[*]](footnote.png) ,
the result is a scalar called the inner
product. For example, if
,
the result is a scalar called the inner
product. For example, if
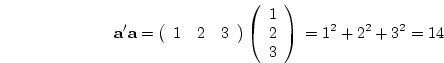 .
This has a simple graphical representation when
.
This has a simple graphical representation when 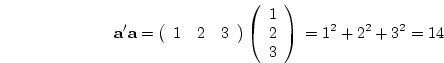 is of
dimension
is of
dimension