



Next: 3 Trace of a
Up: 2 Unary Operations
Previous: 1 Transposition
Index
2 Determinant of a matrix
For a square matrix  we may calculate a scalar called the
determinant which we write as
we may calculate a scalar called the
determinant which we write as 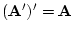 . In the case of a
. In the case of a  matrix, this quantity is calculated as
matrix, this quantity is calculated as
We shall be giving numerical examples of calculating the determinant
when we address matrix inversion. The determinant has an interesting
geometric representation. For example, consider two standardized
variables that correlate  . This situation may be represented
graphically by drawing two vectors, each of length 1.0, having the
same origin and an angle
. This situation may be represented
graphically by drawing two vectors, each of length 1.0, having the
same origin and an angle 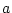 , whose cosine is
, whose cosine is  , between them (see
Figure 4.2).
, between them (see
Figure 4.2).
Figure 4.2:
Geometric representation of the determinant of a matrix. The
angle between the vectors is the cosine of correlation between two
variables, so the determinant is given by twice the area of the
triangle  .
.
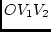 |
It can be shown (the proof involves symmetric square root
decomposition of matrices) that the area of the triangle  is
is
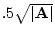 . Thus as the correlation
. Thus as the correlation  increases, the
angle between the lines decreases, the area decreases, and the
determinant decreases. For two variables that correlate perfectly,
the determinant of the correlation (or covariance) matrix is zero.
Conversely, the determinant is at a maximum when
increases, the
angle between the lines decreases, the area decreases, and the
determinant decreases. For two variables that correlate perfectly,
the determinant of the correlation (or covariance) matrix is zero.
Conversely, the determinant is at a maximum when  ; the angle
between the vectors is
; the angle
between the vectors is  , and we say that the variables are
orthogonal. For larger numbers of variables, the determinant is
a function of the hypervolume in n-space; if any single pair of
variables correlates perfectly then the determinant is zero. In
addition, if one of the variables is a linear combination of the
others, the determinant will be zero. For a set of variables with
given variances, the determinant is maximized when all the variables
are orthogonal, i.e., all the off-diagonal elements are zero.
Many software packages [e.g., Mx; SAS, 1985] and numerical
libraries (e.g., IMSL,
1987; NAG, 1990) have algorithms for finding the determinant and
inverse of a matrix. But it is useful to know how matrices can be
inverted by hand, so we present a method for use with paper and
pencil. To calculate the determinant of larger matrices, we employ the
concept of a cofactor. If we delete row
, and we say that the variables are
orthogonal. For larger numbers of variables, the determinant is
a function of the hypervolume in n-space; if any single pair of
variables correlates perfectly then the determinant is zero. In
addition, if one of the variables is a linear combination of the
others, the determinant will be zero. For a set of variables with
given variances, the determinant is maximized when all the variables
are orthogonal, i.e., all the off-diagonal elements are zero.
Many software packages [e.g., Mx; SAS, 1985] and numerical
libraries (e.g., IMSL,
1987; NAG, 1990) have algorithms for finding the determinant and
inverse of a matrix. But it is useful to know how matrices can be
inverted by hand, so we present a method for use with paper and
pencil. To calculate the determinant of larger matrices, we employ the
concept of a cofactor. If we delete row
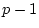 and column
and column 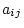 from an
from an 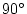 matrix, then the determinant
of the remaining matrix is called the minor of element
matrix, then the determinant
of the remaining matrix is called the minor of element 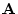 .
The cofactor, written
.
The cofactor, written  is simply:
is simply:
The determinant of the matrix  may be calculated as
may be calculated as
where 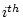 is the order of
is the order of  .
The determinant of a matrix is related to the concept of
definiteness of a matrix. In general, for a null column vector
.
The determinant of a matrix is related to the concept of
definiteness of a matrix. In general, for a null column vector
 , the quadratic form
, the quadratic form 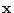 is always zero. For some
matrices, this quadratic is zero only if
is always zero. For some
matrices, this quadratic is zero only if  is the null
vector. If
is the null
vector. If 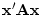 for all non-null vectors
for all non-null vectors  then we
say that the matrix is positive definite.
Conversely, if
then we
say that the matrix is positive definite.
Conversely, if 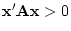 for
all non-null
for
all non-null  , we say that the matrix is negative
definite. However, if we can
find some non-null
, we say that the matrix is negative
definite. However, if we can
find some non-null  such that
such that  then the matrix is
said to be singular, and its determinant
is zero. As long as no two variables are perfectly correlated, and
there are more subjects than measures, a covariance matrix calculated
from data on random variables will be positive definite. Mx
will complain (and rightly so!) if it is given a covariance matrix
that is not positive definite. The determinant of the covariance
matrix can be helpful when there are problems with model-fitting that
seem to originate with the data. However, it is possible to have a
matrix with a positive determinant yet which is negative definite
(consider
then the matrix is
said to be singular, and its determinant
is zero. As long as no two variables are perfectly correlated, and
there are more subjects than measures, a covariance matrix calculated
from data on random variables will be positive definite. Mx
will complain (and rightly so!) if it is given a covariance matrix
that is not positive definite. The determinant of the covariance
matrix can be helpful when there are problems with model-fitting that
seem to originate with the data. However, it is possible to have a
matrix with a positive determinant yet which is negative definite
(consider 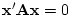 with an even number of rows), so the determinant is
not an adequate diagnostic. Instead we note that all the eigenvalues
of a positive definite matrix are greater than zero. Eigenvalues and
eigenvectors may be obtained from software packages, including Mx, and
the numerical libraries listed above
with an even number of rows), so the determinant is
not an adequate diagnostic. Instead we note that all the eigenvalues
of a positive definite matrix are greater than zero. Eigenvalues and
eigenvectors may be obtained from software packages, including Mx, and
the numerical libraries listed above![[*]](footnote.png) .
.




Next: 3 Trace of a
Up: 2 Unary Operations
Previous: 1 Transposition
Index
Jeff Lessem
2002-03-21
 we may calculate a scalar called the
determinant which we write as
we may calculate a scalar called the
determinant which we write as  . This situation may be represented
graphically by drawing two vectors, each of length 1.0, having the
same origin and an angle
. This situation may be represented
graphically by drawing two vectors, each of length 1.0, having the
same origin and an angle  , between them (see
Figure 4.2).
, between them (see
Figure 4.2).
 increases, the
angle between the lines decreases, the area decreases, and the
determinant decreases. For two variables that correlate perfectly,
the determinant of the correlation (or covariance) matrix is zero.
Conversely, the determinant is at a maximum when
increases, the
angle between the lines decreases, the area decreases, and the
determinant decreases. For two variables that correlate perfectly,
the determinant of the correlation (or covariance) matrix is zero.
Conversely, the determinant is at a maximum when  may be calculated as
may be calculated as
 .
The determinant of a matrix is related to the concept of
definiteness of a matrix. In general, for a null column vector
.
The determinant of a matrix is related to the concept of
definiteness of a matrix. In general, for a null column vector
 , the quadratic form
, the quadratic form  is the null
vector. If
is the null
vector. If  then we
say that the matrix is positive definite.
Conversely, if
then we
say that the matrix is positive definite.
Conversely, if  , we say that the matrix is negative
definite. However, if we can
find some non-null
, we say that the matrix is negative
definite. However, if we can
find some non-null  such that
such that ![[*]](footnote.png) .
.