


Next: 1 Procedure:
Up: 2 Unary Operations
Previous: 3 Trace of a
Index
4 Inverse of a matrix
In ordinary algebra the division operation  is equivalent to
multiplication of the reciprocal
is equivalent to
multiplication of the reciprocal
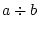 . Thus one
binary operation, division, has been replaced by two operations, one
binary (multiplication) and one unary (forming
. Thus one
binary operation, division, has been replaced by two operations, one
binary (multiplication) and one unary (forming 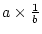 ). In
matrix algebra we make an equivalent substitution of operations, and
we call the unary operation inversion. We write the inverse of
the matrix
). In
matrix algebra we make an equivalent substitution of operations, and
we call the unary operation inversion. We write the inverse of
the matrix  as
as 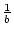 , and calculate it so that
, and calculate it so that
and
where I is the identity matrix. In general the inverse of a
matrix is not simply formed by finding the reciprocal of each element
(this holds only for scalars and diagonal matrices![[*]](footnote.png) ), but is a more complicated operation involving the
determinant.
There are many computer programs available for inverting matrices. Some
routines are general, but there are often faster routines available if the
program is given some information about the matrix, for example, whether it is
symmetric, positive definite, triangular, or diagonal. Here we describe one
general method that is useful for matrix inversion; we recommend
undertaking this hand calculation at least once
for at least a
), but is a more complicated operation involving the
determinant.
There are many computer programs available for inverting matrices. Some
routines are general, but there are often faster routines available if the
program is given some information about the matrix, for example, whether it is
symmetric, positive definite, triangular, or diagonal. Here we describe one
general method that is useful for matrix inversion; we recommend
undertaking this hand calculation at least once
for at least a  matrix in order to fully understand the
concept of a matrix inverse.
matrix in order to fully understand the
concept of a matrix inverse.
Subsections



Next: 1 Procedure:
Up: 2 Unary Operations
Previous: 3 Trace of a
Index
Jeff Lessem
2002-03-21
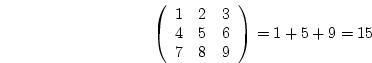 is equivalent to
multiplication of the reciprocal
is equivalent to
multiplication of the reciprocal
 as
as ![[*]](footnote.png) ), but is a more complicated operation involving the
determinant.
There are many computer programs available for inverting matrices. Some
routines are general, but there are often faster routines available if the
program is given some information about the matrix, for example, whether it is
symmetric, positive definite, triangular, or diagonal. Here we describe one
general method that is useful for matrix inversion; we recommend
undertaking this hand calculation at least once
for at least a
), but is a more complicated operation involving the
determinant.
There are many computer programs available for inverting matrices. Some
routines are general, but there are often faster routines available if the
program is given some information about the matrix, for example, whether it is
symmetric, positive definite, triangular, or diagonal. Here we describe one
general method that is useful for matrix inversion; we recommend
undertaking this hand calculation at least once
for at least a