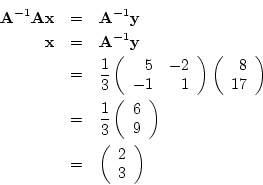Next: 4 Equations in Matrix
Up: 4 Inverse of a
Previous: 4 Inverse of a
Index
In order to invert a matrix, the following four steps can be used:
ex2html_comment_mark>103
0.bean2
- <
- Find the determinant
- <
- Set up the matrix of cofactors
- <
- Transpose the matrix of cofactors
- <
- Divide by the determinant
For example, the matrix
can be inverted by:
ex2html_comment_mark>104
0.bean3
- <
-
- <
-
- <
-
- <
-
To verify this, we can multiply AA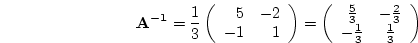 to obtain the identity
matrix:
to obtain the identity
matrix:
The result that
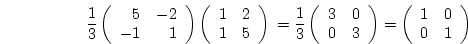 may be used to solve the pair
of simultaneous equations:
may be used to solve the pair
of simultaneous equations:
which may be written
i.e.,
premultiplying both sides by the inverse of  , we have
, we have
which may be verified by substitution.
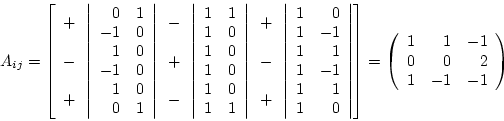
For a larger matrix it is more tedious to compute the inverse. Let us
consider the matrix
ex2html_comment_mark>105
0.bean3
- <
- The determinant is
- <
- The matrix of cofactors is:
- <
- The transpose is
- <
- Dividing by the determinant, we have
which may be verified by multiplication with A to obtain the identity
matrix.




Next: 4 Equations in Matrix
Up: 4 Inverse of a
Previous: 4 Inverse of a
Index
Jeff Lessem
2002-03-21
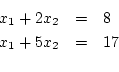
 , we have
, we have