


Next: 5 Applications of Matrix
Up: 4 Matrix Algebra
Previous: 1 Procedure:
Index
4 Equations in Matrix Algebra
Matrix algebra provides a very convenient short hand for writing sets of
equations. For example, the pair of simultaneous equations
may be written
i.e.,
Also if we have the following pair of equations:
then
where  . This is very convenient notation compared with direct
substitution. The Mx structural equations are written in this general
form, i.e.,
. This is very convenient notation compared with direct
substitution. The Mx structural equations are written in this general
form, i.e.,
Real variables (y) = Matrix  hypothetical variables.
hypothetical variables.
To show the simplicity of the matrix notation, consider the following
equations:
Then we have
Similarly, in matrix notation, we have 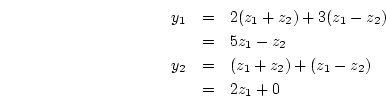 , where
, where
and
or



Next: 5 Applications of Matrix
Up: 4 Matrix Algebra
Previous: 1 Procedure:
Index
Jeff Lessem
2002-03-21
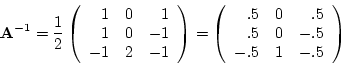
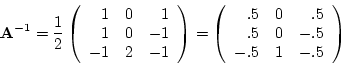
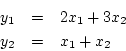
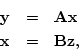
 . This is very convenient notation compared with direct
substitution. The Mx structural equations are written in this general
form, i.e.,
. This is very convenient notation compared with direct
substitution. The Mx structural equations are written in this general
form, i.e.,
hypothetical variables.
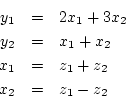
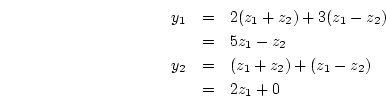 , where
, where