



Next: 3 Assumptions of Path
Up: 5 Path Analysis and
Previous: 1 Introduction
Index
2 Conventions Used in Path Analysis
A path diagram usually consists of boxes and circles, which are
connected by arrows. Consider the diagram in Figure 5.1
for example.
Figure 5.1:
Path diagram for three latent (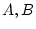 and
and 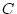 ) and
two observed (
) and
two observed ( and
and 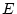 ) variables, illustrating correlations (
) variables, illustrating correlations (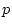 and
and  ) and path coefficients (
) and path coefficients (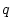 and
and 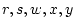 ).
).
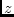 |
Squares or rectangles are used to enclose observed (manifest or
measured) variables, and circles or ellipses surround latent
(unmeasured) variables.
Single-headed arrows
(`paths') are used to define causal relationships in the model, with the
variable at the tail of the arrow causing the variable at the head.
Omission of a path from one variable to another implies that there is
no direct causal influence of the former variable on the latter. In
the path diagram in (Figure 5.1) D is determined by 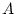 and
and 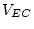 , while
, while 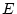 is determined by
is determined by 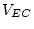 and
and 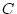 . When two variables
cause each other, we say that there is a feedback-loop, or `reciprocal causation' between them. Such a
feedback-loop is shown between variables D and E in our example.
Double-headed arrows are used to represent a
covariance between two variables, which might arise
through a common cause or their reciprocal causation or both. In many
treatments of path analysis, double-headed arrows may be placed
only between variables that do not have causal arrows pointing at
them. This convention allows us to discriminate between
dependent/endogenous variables and
independent/ultimate/exogenous variables.
Dependent variables are those variables we are trying to predict
(in a regression model) or whose intercorrelations we are trying to
explain (in a factor model). Dependent variables may be determined or
caused by either independent variables or other dependent variables or
both. In Figure 5.1,
. When two variables
cause each other, we say that there is a feedback-loop, or `reciprocal causation' between them. Such a
feedback-loop is shown between variables D and E in our example.
Double-headed arrows are used to represent a
covariance between two variables, which might arise
through a common cause or their reciprocal causation or both. In many
treatments of path analysis, double-headed arrows may be placed
only between variables that do not have causal arrows pointing at
them. This convention allows us to discriminate between
dependent/endogenous variables and
independent/ultimate/exogenous variables.
Dependent variables are those variables we are trying to predict
(in a regression model) or whose intercorrelations we are trying to
explain (in a factor model). Dependent variables may be determined or
caused by either independent variables or other dependent variables or
both. In Figure 5.1,  and
and 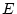 are the dependent
variables. Independent variables are the variables that explain
the intercorrelations between the dependent variables or, in the case
of the simplest regression models, predict the dependent variables.
The causes of independent variables are not represented in the model.
are the dependent
variables. Independent variables are the variables that explain
the intercorrelations between the dependent variables or, in the case
of the simplest regression models, predict the dependent variables.
The causes of independent variables are not represented in the model.
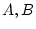 and
and 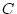 are the independent variables in
Figure 5.1.
Omission of a double-headed arrow reflects the hypothesis that two
independent variables are uncorrelated. In Figure 5.1
the independent variables
are the independent variables in
Figure 5.1.
Omission of a double-headed arrow reflects the hypothesis that two
independent variables are uncorrelated. In Figure 5.1
the independent variables 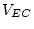 and
and 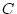 correlate,
correlate, 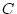 also correlates
with
also correlates
with 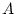 , but
, but 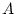 does not correlate with
does not correlate with 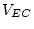 . This illustrates (i)
that two variables which correlate with a third do not necessarily
correlate with each other, and (ii) that when two factors cause the
same dependent variable, it does not imply that they correlate. In
some treatments of path analysis, a double-headed arrow from an
independent variable to itself is used to represent its
variance, but this is often omitted if the variable is
standardized to unit variance. However, for completeness and mathematical
correctness, we do recommend to always include the standardized variance arrows.
By convention, lower-case letters (or numeric values, if these can be
specified) are used to represent the values of paths or double-headed
arrows, in contrast to the use of upper-case for variables. We call
the values corresponding to causal paths path coefficients, and
those of the double-headed arrows simply correlation
coefficients (see Figure 5.1 for examples). In some
applications, subscripts identify the origin and destination of a
path. The first subscript refers to the variable being caused, and
the second subscript tells which variable is doing the causing. In
most genetic applications we assume that the variables are scaled as
deviations from the means, in which case the constant intercept terms
in equations will be zero and can be omitted from the structural
equations.
Each dependent variable usually has a residual, unless it is
fixed to zero ex-hypothesi. The residual
variable does not correlate with any other
determinants of its dependent variable, and will usually (but not
always) be uncorrelated with other independent variables.
In summary therefore, the conventions used in path analysis:
. This illustrates (i)
that two variables which correlate with a third do not necessarily
correlate with each other, and (ii) that when two factors cause the
same dependent variable, it does not imply that they correlate. In
some treatments of path analysis, a double-headed arrow from an
independent variable to itself is used to represent its
variance, but this is often omitted if the variable is
standardized to unit variance. However, for completeness and mathematical
correctness, we do recommend to always include the standardized variance arrows.
By convention, lower-case letters (or numeric values, if these can be
specified) are used to represent the values of paths or double-headed
arrows, in contrast to the use of upper-case for variables. We call
the values corresponding to causal paths path coefficients, and
those of the double-headed arrows simply correlation
coefficients (see Figure 5.1 for examples). In some
applications, subscripts identify the origin and destination of a
path. The first subscript refers to the variable being caused, and
the second subscript tells which variable is doing the causing. In
most genetic applications we assume that the variables are scaled as
deviations from the means, in which case the constant intercept terms
in equations will be zero and can be omitted from the structural
equations.
Each dependent variable usually has a residual, unless it is
fixed to zero ex-hypothesi. The residual
variable does not correlate with any other
determinants of its dependent variable, and will usually (but not
always) be uncorrelated with other independent variables.
In summary therefore, the conventions used in path analysis:
- Observed variables are enclosed in squares or rectangles.
Latent variables are enclosed in circles or ellipses. Error variables
are included in the path diagram, and may be enclosed by circles or
ellipses or (occasionally) not enclosed at all.
- Upper-case letters are used to denote observed or latent
variables, and lower-case letters or numeric values represent the
values of paths or two-way arrows, respectively called path
coefficients and correlation coefficients.
- A one-way arrow between two variables indicates a postulated
direct influence of one variable on another. A two-way arrow between
two variables indicates that these variables may be correlated without
any assumed direct relationship.
- There is a fundamental distinction between independent variables
and dependent variables. Independent variables are not caused by any
other variables in the system.
- Coefficients may have two subscripts, the first indicating the
variable to which arrow points, the second showing its origin.




Next: 3 Assumptions of Path
Up: 5 Path Analysis and
Previous: 1 Introduction
Index
Jeff Lessem
2002-03-21