



Next: 3 Fitting the Multivariate
Up: 3 Simple Genetic Factor
Previous: 1 Multivariate Genetic Factor
Index
2 Alternate Representation of the Multivariate
Genetic Factor Model
One of the features of Mx is its flexibility for specifying the same or
very similar models in different ways. Frequently the choice of model
specification is simply a matter of individual preference, convenience, or
familiarity with Mx notation, particularly when a model can be written in
several different ways with no change in the substantive or numerical
outcome. However, at other times very subtle changes in the Mx
formulation of a model translate into a completely different substantive
question. While it may be true that flexibility imparts confusion, it is
important to recognize and distinguish alternative representations of
genetic models in Mx.
While the approach discussed above may be fairly intuitive, the
B matrix may become relatively big, therefore increasing the chance of
errors in editing. An alternative approach is to specify the common
factors and residual variances for genetic, shared and specific
environmental factors in separate matrices. One advantage of this
approach is that the model can be easily adapted for a different number of
common factors or observed variables. For example, if we use a 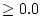 matrix X for the genetic common factor, a
matrix X for the genetic common factor, a 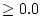 matrix Y
for the shared environmental common factor, a
matrix Y
for the shared environmental common factor, a 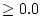 matrix Z
for the specific environmental common factor and a
matrix Z
for the specific environmental common factor and a  diagonal
matrix F for the unique variances, the matrices section in Mx would
be
diagonal
matrix F for the unique variances, the matrices section in Mx would
be X Full 4 1 Free ! genetic common factor Y Full 4 1
Free ! shared environmental common factor Z Full 4 1 Free ! specific
environmental common factor F Diag 4 4 Free ! specific environmental
unique variances
We can then pre-calculate the genetic,
shared and specific environmental variance components in the algebra
section: A= X*X'; C= Y*Y'; E= Z*Z' +F*F';
and these matrices can be used to specify the expected
covariance matrices for MZ and DZ twins in a similar fashion as the
univariate models. Note that by using a Kronecker product for the genetic
variance component in DZ twins (H@A) every element of the
A matrix is multiplied by one half. One additional feature in Mx
that allows for flexible model specification is the #define
statement. One possible use is to define the number of variables up
front, e.g.
#define nvar 4
and use the 'defined' variables in the matrices section:
X Full nvar 1 Free ! genetic common factor
Y Full nvar 1 Free ! shared environmental common factor
Z Full nvar 1 Free ! specific environmental common factor
F Diag nvar nvar Free ! specific environmental unique variances
If we wanted to do an analysis with just three variables, the only
change to be made, besides the NInput_vars and Select
statements, is the #define statement.




Next: 3 Fitting the Multivariate
Up: 3 Simple Genetic Factor
Previous: 1 Multivariate Genetic Factor
Index
Jeff Lessem
2002-03-21