



Next: 3 Analyzing Developmental Change
Up: 5 Relationships between Variables
Previous: 1 Contribution of Genes
Index
2 Analyzing Direction of Causation
Students of elementary statistics have long been made to
recite ``correlation does not imply causation'' and rightly
so, because a premature assignment of causality to a mere
statistical association could waste scientific resources and do
actual harm if treatment were to be based upon it. However, one
of the goals of science is to analyze complex systems into
elementary processes which are thought to be causal or more
fundamental and, when actual experimental intervention is
difficult, it may be necessary to look to the nexus of
intercorrelations among measures for clues about causality.
The claim that correlation does not imply causality comes
from a fundamental indeterminacy of any general model for the
correlation between a single pair of variables. Put simply, if
we observe a correlation between 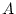 and
and 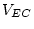 , it can arise from one
or all of three processes:
, it can arise from one
or all of three processes: 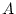 causing
causing 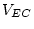 (denoted
(denoted
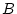 ),
), 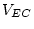 causing
causing 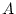 , or
latent variable
, or
latent variable  causing
causing 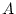 and
and 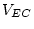 . A general model for the
correlation between
. A general model for the
correlation between 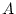 and
and 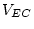 would need constants to account for
the strength of the causal connections between
would need constants to account for
the strength of the causal connections between 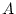 and
and 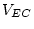 ,
, 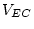 and
and 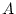 ,
,
 and
and 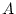 ,
,  and
and 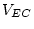 . Clearly, a single correlation cannot be used
to determine four unknown parameters.
When we have more than two variables, however, matters may
look a little different. It may now become possible to exclude
some causal hypotheses as clearly inconsistent with the data.
Whether or not this can be done will depend on the complexity of
the causal nexus being analyzed. For example, a pattern of
correlations of
the form
. Clearly, a single correlation cannot be used
to determine four unknown parameters.
When we have more than two variables, however, matters may
look a little different. It may now become possible to exclude
some causal hypotheses as clearly inconsistent with the data.
Whether or not this can be done will depend on the complexity of
the causal nexus being analyzed. For example, a pattern of
correlations of
the form
 would support one or other of
the causal
sequences
would support one or other of
the causal
sequences
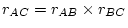 or
or
 in preference to orders that place A or C in
the middle.
The fact that causality implies temporal priority has been
used in some applications to advocate a longitudinal strategy for
its analysis. One approach is the cross-lagged panel
study in which the variables A and B are measured at
two points in time,
in preference to orders that place A or C in
the middle.
The fact that causality implies temporal priority has been
used in some applications to advocate a longitudinal strategy for
its analysis. One approach is the cross-lagged panel
study in which the variables A and B are measured at
two points in time, 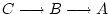 and
and 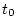 . If the
correlation of A at
. If the
correlation of A at 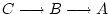 with B at
with B at 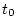 is greater than the
correlation of B at
is greater than the
correlation of B at 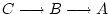 with A at
with A at 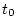 , we might give some credence
to the causal priority of A over B. Methods for the statistical
assessment of such relative priorities are
known as ``cross-lagged panel analysis'' [] and may
assessed within structural equation models [].
The cross-lagged approach, though strongly suggestive of
causality in some circumstances, is not entirely foolproof. With
this fact in view, researchers are always on the look-out for
other approaches that can be used to test hypotheses about
causality in correlational data. It has recently become clear
that the cross-sectional twin study, in which multiple measures
are made only on one occasion, may, under some circumstances,
allow us to test hypotheses about direction of causality without
the necessity of longitudinal data. The potential contribution
of twin studies to resolving alternative models of causation will
be discussed in Chapter
, we might give some credence
to the causal priority of A over B. Methods for the statistical
assessment of such relative priorities are
known as ``cross-lagged panel analysis'' [] and may
assessed within structural equation models [].
The cross-lagged approach, though strongly suggestive of
causality in some circumstances, is not entirely foolproof. With
this fact in view, researchers are always on the look-out for
other approaches that can be used to test hypotheses about
causality in correlational data. It has recently become clear
that the cross-sectional twin study, in which multiple measures
are made only on one occasion, may, under some circumstances,
allow us to test hypotheses about direction of causality without
the necessity of longitudinal data. The potential contribution
of twin studies to resolving alternative models of causation will
be discussed in Chapter ![[*]](crossref.png) . At this stage, however, it is
sufficient to give a simple insight about one set of
circumstances which might lead us to prefer one causal hypothesis
over another.
Consider the ambiguous relationship between exercise and
body weight. In free-living populations, there is a significant
correlation between exercise and body weight. How much of that
association is due to the fact that people who exercise use up
more calories and how much to the fact that fat people don't
like jogging? In the simplest possible case, suppose that we
found variation in exercise to be purely environmental (i.e.,
having no genetic component) and variation in weight to be partly
genetic. Then there is no way that the direction of causation
can go from body weight to exercise because, if this were the
case, some of the genetic effects on body weight would create
genetic variation in exercise. In practice, things are seldom
that simple. Data are nearly always more ambiguous and
hypotheses more complex. But this simple example illustrates
that the genetic studies, notably the twin study, may sometimes
yield valuable insight about the causal relationships between
multiple variables.
. At this stage, however, it is
sufficient to give a simple insight about one set of
circumstances which might lead us to prefer one causal hypothesis
over another.
Consider the ambiguous relationship between exercise and
body weight. In free-living populations, there is a significant
correlation between exercise and body weight. How much of that
association is due to the fact that people who exercise use up
more calories and how much to the fact that fat people don't
like jogging? In the simplest possible case, suppose that we
found variation in exercise to be purely environmental (i.e.,
having no genetic component) and variation in weight to be partly
genetic. Then there is no way that the direction of causation
can go from body weight to exercise because, if this were the
case, some of the genetic effects on body weight would create
genetic variation in exercise. In practice, things are seldom
that simple. Data are nearly always more ambiguous and
hypotheses more complex. But this simple example illustrates
that the genetic studies, notably the twin study, may sometimes
yield valuable insight about the causal relationships between
multiple variables.




Next: 3 Analyzing Developmental Change
Up: 5 Relationships between Variables
Previous: 1 Contribution of Genes
Index
Jeff Lessem
2002-03-21
![[*]](crossref.png) . At this stage, however, it is
sufficient to give a simple insight about one set of
circumstances which might lead us to prefer one causal hypothesis
over another.
Consider the ambiguous relationship between exercise and
body weight. In free-living populations, there is a significant
correlation between exercise and body weight. How much of that
association is due to the fact that people who exercise use up
more calories and how much to the fact that fat people don't
like jogging? In the simplest possible case, suppose that we
found variation in exercise to be purely environmental (i.e.,
having no genetic component) and variation in weight to be partly
genetic. Then there is no way that the direction of causation
can go from body weight to exercise because, if this were the
case, some of the genetic effects on body weight would create
genetic variation in exercise. In practice, things are seldom
that simple. Data are nearly always more ambiguous and
hypotheses more complex. But this simple example illustrates
that the genetic studies, notably the twin study, may sometimes
yield valuable insight about the causal relationships between
multiple variables.
. At this stage, however, it is
sufficient to give a simple insight about one set of
circumstances which might lead us to prefer one causal hypothesis
over another.
Consider the ambiguous relationship between exercise and
body weight. In free-living populations, there is a significant
correlation between exercise and body weight. How much of that
association is due to the fact that people who exercise use up
more calories and how much to the fact that fat people don't
like jogging? In the simplest possible case, suppose that we
found variation in exercise to be purely environmental (i.e.,
having no genetic component) and variation in weight to be partly
genetic. Then there is no way that the direction of causation
can go from body weight to exercise because, if this were the
case, some of the genetic effects on body weight would create
genetic variation in exercise. In practice, things are seldom
that simple. Data are nearly always more ambiguous and
hypotheses more complex. But this simple example illustrates
that the genetic studies, notably the twin study, may sometimes
yield valuable insight about the causal relationships between
multiple variables.