



Next: 2 Transformations of Data
Up: 5 Applications of Matrix
Previous: 5 Applications of Matrix
Index
1 Calculation of Covariance Matrix from Data Matrix
Suppose we have a data matrix  with rows corresponding to
subjects and columns corresponding to variables. We can calculate a
mean for each variable and replace the data matrix with a matrix of
deviations from the mean. That is, each element
with rows corresponding to
subjects and columns corresponding to variables. We can calculate a
mean for each variable and replace the data matrix with a matrix of
deviations from the mean. That is, each element 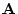 is
replaced by
is
replaced by
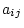 where
where 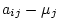 is the mean of the
is the mean of the
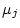 variable. Let us call the new matrix
variable. Let us call the new matrix 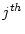 . The
covariance matrix is then simply calculated as
. The
covariance matrix is then simply calculated as
where  is the number of subjects.
For example, suppose we have the following data:
is the number of subjects.
For example, suppose we have the following data:
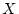 |
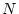 |
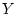 |
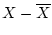 |
| 1 |
2 |
-2 |
-4 |
| 2 |
8 |
-1 |
2 |
| 3 |
6 |
0 |
0 |
| 4 |
4 |
1 |
-2 |
| 5 |
10 |
2 |
4 |
So the matrix of deviations from the mean is
and therefore the covariance matrix of the observations is
The diagonal elements of this matrix are the variances of the variables, and
the off-diagonal elements are the covariances between the variables. The
standard deviation is the square root of the variance (see
Chapter 2).
The correlation is
In general, a correlation matrix may be calculated from a covariance
matrix by pre- and post-multiplying the covariance matrix by a
diagonal matrix  in which each diagonal element
in which each diagonal element 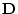 is
is
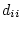 , i.e., the reciprocal of the standard deviation for
that variable. Thus, in our two variable example, we have:
, i.e., the reciprocal of the standard deviation for
that variable. Thus, in our two variable example, we have:




Next: 2 Transformations of Data
Up: 5 Applications of Matrix
Previous: 5 Applications of Matrix
Index
Jeff Lessem
2002-03-21
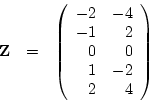
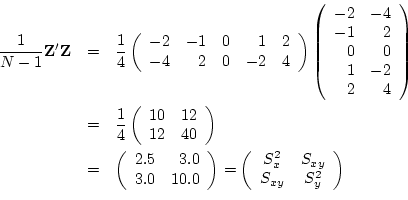
 in which each diagonal element
in which each diagonal element