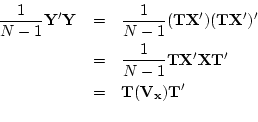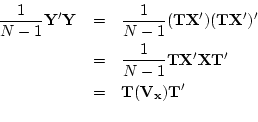


Next: 2 Unary operations
Up: 6 Exercises
Previous: 6 Exercises
Index
Let
ex2html_comment_mark>112
0.bean1
- <
- Form AB.
- <
- Form BA. (Careful, this might be a trick question!)
Let
- 1.
- Form
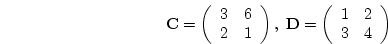 .
.
- 2.
- Form
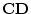 .
.
- 3.
- In ordinary algebra, multiplication is commutative, i.e.
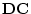 .
In general, is matrix multiplication commutative?
.
In general, is matrix multiplication commutative?
Let
- 4.
- Form
 .
.
- 5.
- Form
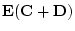 .
.
- 6.
- In ordinary algebra, multiplication is distributive over addition,
i.e.
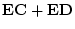 .
In general, is matrix multiplication distributive over matrix addition?
Is matrix multiplication distributive over matrix subtraction?
.
In general, is matrix multiplication distributive over matrix addition?
Is matrix multiplication distributive over matrix subtraction?
Jeff Lessem
2002-03-21