


Next: 8 Incorporating Data from
Up: 6 Univariate Analysis
Previous: 6 Interpreting Univariate Results
Index
7 Testing the Equality of Means
Applications of structural equation modeling to twin and other family
data typically tend to ignore means. That is, observed measures are
treated as deviations from the phenotypic mean (and are thus termed
deviation phenotypes)![[*]](footnote.png) , and likewise
genotypic and environmental latent variables are expressed as
deviations from their means, which usually are fixed at 0. Most
simple genetic models predict the same mean for different groups of
relatives, so, for example, MZ twins, DZ twins, males from
opposite-sex twin pairs, and males from like-sex twin pairs should
have (within sampling error) equal means. Where significant mean
differences are found, they may indicate sampling problems with
respect to the variable under study or other violations of the
assumptions of the basic genetic model. Testing for mean differences
also may be important in follow-up studies, where we are concerned
about the bias introduced by sample attrition, but can compare mean
scores at baseline for those relatives who remain in a study with
those who drop out. Fortunately, Mx facilitates tests for mean
differences between groups.
, and likewise
genotypic and environmental latent variables are expressed as
deviations from their means, which usually are fixed at 0. Most
simple genetic models predict the same mean for different groups of
relatives, so, for example, MZ twins, DZ twins, males from
opposite-sex twin pairs, and males from like-sex twin pairs should
have (within sampling error) equal means. Where significant mean
differences are found, they may indicate sampling problems with
respect to the variable under study or other violations of the
assumptions of the basic genetic model. Testing for mean differences
also may be important in follow-up studies, where we are concerned
about the bias introduced by sample attrition, but can compare mean
scores at baseline for those relatives who remain in a study with
those who drop out. Fortunately, Mx facilitates tests for mean
differences between groups.
For Mx to fit a model to means and covariances, both observed means
and a model for them must be supplied.
Appendix ![[*]](crossref.png) contains a Mx script for fitting a univariate
genetic model which also estimates the means of first and second twins
from MZ and DZ pairs. The first change we make is to feed Mx the
observed means in our sample, which we do with the
contains a Mx script for fitting a univariate
genetic model which also estimates the means of first and second twins
from MZ and DZ pairs. The first change we make is to feed Mx the
observed means in our sample, which we do with the Means command:
Means 0.9087 0.8685
Second, we declare a matrix for the means, e.g. M Full 1 2 in
the matrices section. Third, we can equate parameters for the first
and second twins by using a Specify statement such as
Specify M 101 101
where 101 is a parameter number that has not been used
elsewhere in the script. By using the same number for the two means,
they are constrained to be equal. Fourth, we include a model for the
means:
Means M;
In the DZ group we also supply the observed means, and adjust the
model for the means.
We can then either (i) equate the mean for MZ twins to that for DZ
twins by using the same matrix M, 'copied' from the MZ group or
equated to that of the MZ group as follows:
M Full 1 2 = M2
where M2 refers to matrix M in group 2; to fit a no
heterogeneity model; or (ii) equate DZ twin 1 and DZ twin 2 means
but allow them to differ from the MZ means by declaring a new matrix
(possible called M too) to fit a zygosity dependent means model
(
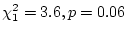 ); or (iii) estimate four means,
i.e., first and second twins in each of the MZ and DZ groups. This
third option gives a perfect fit to the data with regard to mean
structure, so that the only contribution to the fit function comes
from the covariance structure. Hence the four means model gives the
same goodness-of-fit
); or (iii) estimate four means,
i.e., first and second twins in each of the MZ and DZ groups. This
third option gives a perfect fit to the data with regard to mean
structure, so that the only contribution to the fit function comes
from the covariance structure. Hence the four means model gives the
same goodness-of-fit 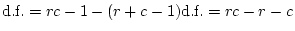 as in the analyses ignoring means.
as in the analyses ignoring means.
Table 6.6 reports the results of fitting models
incorporating means
Table 6.6:
Results of fitting models to twin pair covariance matrices and twin
means for Body Mass index: Two-group analyses, complete pairs only.
| |
|
Female |
Male |
| |
|
Young |
Older |
Young |
Older |
| Model |
df |
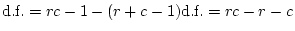 |
|
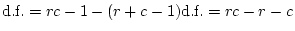 |
|
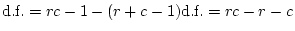 |
|
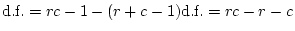 |
|
| 1. No heterogeneity |
|
|
|
|
|
|
|
|
|
| of means |
6 |
7.84 |
.25 |
5.74 |
.57 |
12.81 |
.05 |
5.69 |
.58 |
| 2. Heterogeneity |
|
|
|
|
|
|
|
|
|
| MZ vs DZ |
5 |
3.93 |
.56 |
4.75 |
.58 |
7.72 |
.17 |
5.36 |
.50 |
| 3. Heterogeneity |
|
|
|
|
|
|
|
|
|
| MZ/DZ & T1/T2 |
3 |
3.71 |
.29 |
2.38 |
.67 |
7.28 |
.06 |
5.03 |
.17 |
| Genetic Model |
|
ADE |
AE |
ADE |
AE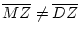 |
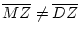 AE models have one more degree of freedom than shown in the df column
AE models have one more degree of freedom than shown in the df column
to the like-sex twin pair data on BMI. In each analysis, we have
considered only the best-fitting genetic model identified in the
analyses ignoring means. Again we subtract the 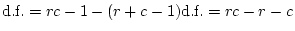 of a more
general model from the
of a more
general model from the 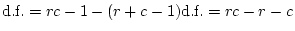 of a more restricted model to get a
likelihood ratio test of the difference in fit between the two. For
the two older cohorts we find no evidence for mean differences either
between zygosity groups or between first and second twins. That is,
the model that assumes no heterogeneity of means (model 1) does not
give a significantly worse fit than either (i) estimating separate MZ
and DZ means (model 2), or (ii) estimating 4 means. For older
females, likelihood-ratio chi-squares are
of a more restricted model to get a
likelihood ratio test of the difference in fit between the two. For
the two older cohorts we find no evidence for mean differences either
between zygosity groups or between first and second twins. That is,
the model that assumes no heterogeneity of means (model 1) does not
give a significantly worse fit than either (i) estimating separate MZ
and DZ means (model 2), or (ii) estimating 4 means. For older
females, likelihood-ratio chi-squares are
 and
and
 ; and for older males,
; and for older males,
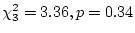 and
and
 .
Maximum-likelihood estimates of mean log BMI in the older cohort are,
respectively, 21.87 and 22.26 for females and males; estimates of
genetic and environmental parameters are unchanged from those obtained
in the analyses ignoring means. In the younger cohorts, however, we
do find significant mean differences between zygosity groups, both in
females (
.
Maximum-likelihood estimates of mean log BMI in the older cohort are,
respectively, 21.87 and 22.26 for females and males; estimates of
genetic and environmental parameters are unchanged from those obtained
in the analyses ignoring means. In the younger cohorts, however, we
do find significant mean differences between zygosity groups, both in
females (
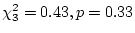 ) and in males
(
) and in males
(
 ). In both sexes, mean log BMI values
are lower in MZ pairs (21.35 for females, 21.63 for males) than for DZ
pairs (21.45 for females, 21.79 for males). As these data are not
age-corrected, it is possible that BMI values are still changing in
this age-group, and that the zygosity difference reflects a slight
mean difference in age. We shall return to this question in
Section 6.9.
). In both sexes, mean log BMI values
are lower in MZ pairs (21.35 for females, 21.63 for males) than for DZ
pairs (21.45 for females, 21.79 for males). As these data are not
age-corrected, it is possible that BMI values are still changing in
this age-group, and that the zygosity difference reflects a slight
mean difference in age. We shall return to this question in
Section 6.9.



Next: 8 Incorporating Data from
Up: 6 Univariate Analysis
Previous: 6 Interpreting Univariate Results
Index
Jeff Lessem
2000-03-20
![[*]](footnote.png) , and likewise
genotypic and environmental latent variables are expressed as
deviations from their means, which usually are fixed at 0. Most
simple genetic models predict the same mean for different groups of
relatives, so, for example, MZ twins, DZ twins, males from
opposite-sex twin pairs, and males from like-sex twin pairs should
have (within sampling error) equal means. Where significant mean
differences are found, they may indicate sampling problems with
respect to the variable under study or other violations of the
assumptions of the basic genetic model. Testing for mean differences
also may be important in follow-up studies, where we are concerned
about the bias introduced by sample attrition, but can compare mean
scores at baseline for those relatives who remain in a study with
those who drop out. Fortunately, Mx facilitates tests for mean
differences between groups.
, and likewise
genotypic and environmental latent variables are expressed as
deviations from their means, which usually are fixed at 0. Most
simple genetic models predict the same mean for different groups of
relatives, so, for example, MZ twins, DZ twins, males from
opposite-sex twin pairs, and males from like-sex twin pairs should
have (within sampling error) equal means. Where significant mean
differences are found, they may indicate sampling problems with
respect to the variable under study or other violations of the
assumptions of the basic genetic model. Testing for mean differences
also may be important in follow-up studies, where we are concerned
about the bias introduced by sample attrition, but can compare mean
scores at baseline for those relatives who remain in a study with
those who drop out. Fortunately, Mx facilitates tests for mean
differences between groups.
![[*]](crossref.png)