


Next: 9 Conclusions: Genetic Analyses
Up: 6 Univariate Analysis
Previous: 7 Testing the Equality
Index
8 Incorporating Data from Singleton Twins
In most twin studies, there are many twin pairs in which only one twin
agrees to cooperate. We call these pairs discordant-participant as opposed to concordant-participant
pairs, in which data are collected from both members of the pair.
Sadly, data from discordant-participant pairs are often just thrown
away. This is unfortunate not only because of the wasted effort on
the part of the twins, researchers, and data entry personnel, but also
because they provide valuable information about the representativeness
of the sample for the variable under study. If sampling is
satisfactory, then we would expect to find the same mean and variance
in concordant-participant pairs as in discordant-participant pairs.
Thus, the presence of mean differences or variance differences between
these groups is an indication that biased sampling may have occurred
with respect to the variable under investigation. To take a concrete
example, suppose that overweight twins are less likely to respond to a
mailed questionnaire survey. Given the strong twin pair resemblance
for BMI demonstrated in previous sections, we might expect to find
that individuals from discordant-participant pairs are on average
heavier than individuals from concordant-participant pairs. Such
sampling biases will have differential effects on the covariances of
MZ and DZ twin pairs, and thus may lead to biased estimates of genetic
and environmental parameters (Lykken et al., 1987;
Neale et al., 1989b).
Table 6.7 reports means and variances for transformed BMI from
Table 6.7:
Means and variances for Body Mass Index of twins whose cotwin
did not cooperate in the 1981 Australian survey.
| |
| |
Young Cohort (=30) |
|
Older
Cohort (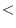 30) 30) |
| Group |
N |
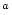 |
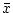 |
|
N |
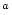 |
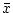 |
| MZ Female Twins |
33 |
0.1795 |
1.0640 |
|
44 |
0.6852 |
1.1461 |
| DZ Female Twins |
55 |
0.5836 |
0.8983 |
|
62 |
1.0168 |
1.7357 |
| MZ Male Twins |
24 |
1.3266 |
1.2477 |
|
36 |
1.3585 |
1.1036 |
| DZ Male Twins |
47 |
1.2705 |
1.5309 |
|
48 |
1.0379 |
1.6716 |
| Opp-Sex Pair Females |
65 |
0.6551 |
1.4390 |
|
81 |
0.9756 |
1.2690 |
| Opp-Sex Pair Males |
28 |
0.8724 |
0.9754 |
|
27 |
1.7149 |
1.0019 |
individuals from discordant-participant pairs in the 1981 Australian
survey. Zygosity assignment for MZ twins must be regarded as somewhat
tentative, since most algorithms for zygosity diagnosis based on
questionnaire data require reports from both members of a twin pair to
confirm monozygosity (e.g., Eaves et al.,
1989b). In most groups, comparing
Table 6.7 to Table 6.3, we observe both higher
means and higher variances in the discordant-participant pairs. It is
clearly important to test whether these differences are statistically
significant.
To fit a model simultaneously to the means, variances, and covariances
of concordant-participant pairs and the means and variances of
discordant-participant pairs, requires that we analyze data where
there are different numbers of observed variables per group, which is
easily done in Mx.
Appendix ![[*]](crossref.png) presents a Mx script for testing for
differences in mean or variance. We constrain the means of the
responding twin in groups four (MZ discordant-participant) and five
(DZ discordant-participant) to equal those of twins from the
concordant-participant pairs. Our test for significant difference in
means between the concordant-participant and discordant-participant
groups is the improvement in goodness-of-fit obtained when we allow
these latter, discordant-participant pairs, to take their own mean
value.
presents a Mx script for testing for
differences in mean or variance. We constrain the means of the
responding twin in groups four (MZ discordant-participant) and five
(DZ discordant-participant) to equal those of twins from the
concordant-participant pairs. Our test for significant difference in
means between the concordant-participant and discordant-participant
groups is the improvement in goodness-of-fit obtained when we allow
these latter, discordant-participant pairs, to take their own mean
value.
Table 6.8 summarizes the results of model-fitting. For
these analyses, we considered only the best-fitting genetic model
based on the results of the analyses ignoring means, and allowed for
zygosity differences in mean only if these were found to be
significant in the analyses of the previous Section (i.e., in the
younger twin pairs; young female pairs are the only group in
which we find no difference between concordant-participant pairs and
discordant-participant pairs). In the two older cohorts a
model allowing for heterogeneity of means (Model 3) gives a
substantially better fit than one that assumes no heterogeneity of
means or variances (Model 1: older females:
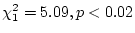 ; older males:
; older males:
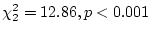 ). Specifying
heterogeneity of variances in addition to heterogeneity of means does
not produce a further improvement in fit (older females:
). Specifying
heterogeneity of variances in addition to heterogeneity of means does
not produce a further improvement in fit (older females:
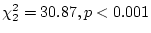 ; older males:
; older males:
 ).
Such a result is not atypical because the power to detect differences
in mean is much greater than that to detect a difference in variance.
).
Such a result is not atypical because the power to detect differences
in mean is much greater than that to detect a difference in variance.
Table 6.8:
Results
of fitting models to twin pair covariance matrices and twin
means for Body Mass Index: Two like-sex twin groups, plus data from twins from
incomplete pairs. Models test for heterogeneity of means or variances between
twins from pairs concordant vs discordant for cooperation in 1981 survey.
| |
|
Female |
Male |
|
| |
|
Young |
Older |
Young |
Older |
|
| Model |
df |
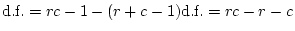 |
|
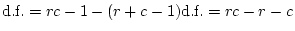 |
|
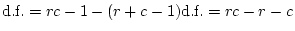 |
|
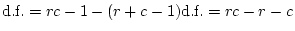 |
|
|
1. No heterogen.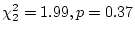
|
11 |
8.16 |
.70 |
20.62 |
.08 |
54.97 |
.001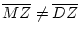 |
48.55 |
.001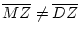 |
|
| of means or variances |
|
|
|
|
|
|
|
|
2. Heterogeneity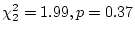 |
9 |
6.03 |
.74 |
17.84 |
.09 |
29.22 |
.001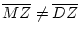 |
44.58 |
.001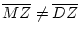 |
|
| of means |
|
|
|
|
|
|
|
|
3. Heterogeneity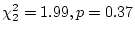
|
9 |
5.70 |
.77 |
7.76 |
.74 |
22.76 |
.01 |
7.68 |
.74 |
|
| of variances |
|
|
|
|
|
|
|
|
| 4. Heterogeneity
|
7 |
3.93 |
.79 |
5.74 |
.77 |
7.72 |
.36 |
5.69 |
.77 |
|
| of means and variances |
|
|
|
|
|
|
|
|
| Genetic Model |
|
ADE |
AE# |
ADE |
AE# |
|
| Means Model |
|
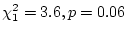 |
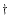 |
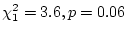 |
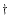 |
|
 Between concordant-participant versus
discordant-participant twins. Between concordant-participant versus
discordant-participant twins. |
|
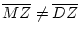  . . |
|
| # AE models have two more degrees of freedom than shown in the df column |
|
When considering these results, we must bear in mind several
possibilities. Numbers of twins from the discordant-participant
groups are small, and estimates of mean and variance in these groups
will be particularly vulnerable to outlier-effects; that is, to
inflation by one or two individuals of very high BMI. Further outlier
analyses (e.g., Bollen, 1989) would be needed to determine whether
this is an explanation of the variance difference. In the young
males, it is also possible that age differences between
concordant-participant pairs and discordant-participant pairs could
generate the observed mean differences.



Next: 9 Conclusions: Genetic Analyses
Up: 6 Univariate Analysis
Previous: 7 Testing the Equality
Index
Jeff Lessem
2000-03-20
![[*]](crossref.png)