



Next: 5 Loss of Power
Up: 7 Power and Sample
Previous: 3 Steps in Power
Index
4 Power for the continuous case
A common question in genetic
research concerns the ability of a study of twins reared together to
detect the effects of the shared environment. Let us investigate this
issue using Mx. Following the steps outlined above, we start by
stipulating that we are going to explore the power of a classical twin
study -- that is, one in which we measure MZ and DZ twins reared
together. We shall assume that 50% of the variation in the
population is due to the unique environmental experiences of
individuals (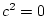 ). The expected MZ twin correlation is
therefore 0.50. This intermediate value is chosen to be typical of
many of the less-familial traits. Anthropometric traits, and many
cognitive traits, tend to have higher MZ correlations than this, so
the power calculations should be conservative as far as such variables
are concerned. We assume further that the additive genetic component
explains 30% of the total variation (
). The expected MZ twin correlation is
therefore 0.50. This intermediate value is chosen to be typical of
many of the less-familial traits. Anthropometric traits, and many
cognitive traits, tend to have higher MZ correlations than this, so
the power calculations should be conservative as far as such variables
are concerned. We assume further that the additive genetic component
explains 30% of the total variation ( ) and that the
shared family environment accounts for the remaining 20%
(
) and that the
shared family environment accounts for the remaining 20%
(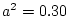 ). We now substitute these parameter values into the
algebraic expectations for the variances and covariances of MZ and DZ
twins:
). We now substitute these parameter values into the
algebraic expectations for the variances and covariances of MZ and DZ
twins:
| Total variance |
= |
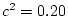 |
= |
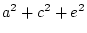 |
= |
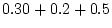 |
| MZ
covariance |
= |
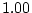 |
= |
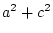 |
= |
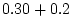 |
| DZ covariance |
= |
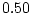 |
= |
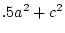 |
= |
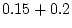 |
In Appendix ![[*]](crossref.png) we show a version of the Mx code for
fitting the ACE model to the simulated covariance matrices. In
addition to the expected covariances we must assign an arbitrary
sample size and structure. Initially, we shall assume the study
involves equal numbers, 1000 each, of MZ and DZ pairs. In order to
conduct the power calculations for the
we show a version of the Mx code for
fitting the ACE model to the simulated covariance matrices. In
addition to the expected covariances we must assign an arbitrary
sample size and structure. Initially, we shall assume the study
involves equal numbers, 1000 each, of MZ and DZ pairs. In order to
conduct the power calculations for the 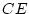 component, we can run the
job for the full (ACE) model first and then the AE
model, obtaining the expected difference in
component, we can run the
job for the full (ACE) model first and then the AE
model, obtaining the expected difference in  under the full and reduced models just as we did earlier for testing
the significance of the shared environment in real data.
Notice that fitting the full ACE model yields a goodness-of-fit
under the full and reduced models just as we did earlier for testing
the significance of the shared environment in real data.
Notice that fitting the full ACE model yields a goodness-of-fit
 of zero. This should always be the case when we use Mx
to solve for all the parameters of the model we used to generate the
expected covariance matrices because, since there is no sampling error
attached to the simulated covariance matrices, there is perfect
agreement between the matrices supplied as ``data" and the expected
values under the model. In addition, the parameter estimates obtained
should agree precisely with those used to simulate the data; if they
are not, but the fit is still perfect, it suggests that the model is
not identified (see Section 5.7) Therefore, as long
as we are confident that we have specified the structural model
correctly and that the full model is identified, there is really no
need to fit the full model to the simulated covariances matrices since
we know in advance that the ``
of zero. This should always be the case when we use Mx
to solve for all the parameters of the model we used to generate the
expected covariance matrices because, since there is no sampling error
attached to the simulated covariance matrices, there is perfect
agreement between the matrices supplied as ``data" and the expected
values under the model. In addition, the parameter estimates obtained
should agree precisely with those used to simulate the data; if they
are not, but the fit is still perfect, it suggests that the model is
not identified (see Section 5.7) Therefore, as long
as we are confident that we have specified the structural model
correctly and that the full model is identified, there is really no
need to fit the full model to the simulated covariances matrices since
we know in advance that the `` " is expected to be zero. In
practice it is often helpful to recover this known result to increase
our confidence that both we and the software are doing the right
thing.
For our specific case, with samples of 1000 MZ and DZ pairs, we obtain
a goodness-of-fit
" is expected to be zero. In
practice it is often helpful to recover this known result to increase
our confidence that both we and the software are doing the right
thing.
For our specific case, with samples of 1000 MZ and DZ pairs, we obtain
a goodness-of-fit 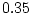 of 11.35 for the AE model. Since the
full model yields a perfect fit (
of 11.35 for the AE model. Since the
full model yields a perfect fit (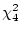 ), the expected
difference in
), the expected
difference in  for 1 df -- testing for the effect of the
shared environment -- is 11.35. Such a value is well in excess of
the 3.84 necessary to conclude that
for 1 df -- testing for the effect of the
shared environment -- is 11.35. Such a value is well in excess of
the 3.84 necessary to conclude that 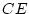 is significant at the 5%
level. However, this is only the value expected in the ideal
situation. With real data, individual
is significant at the 5%
level. However, this is only the value expected in the ideal
situation. With real data, individual  values will vary
greatly as a function of sampling variance. We need to choose the
sample sizes to give an expected value of
values will vary
greatly as a function of sampling variance. We need to choose the
sample sizes to give an expected value of  such that observed
values exceed 3.84 in a specified proportion of cases corresponding to
the desired power of the test.
It turns out that such problems are very familiar to statisticians and
that the expected values of
such that observed
values exceed 3.84 in a specified proportion of cases corresponding to
the desired power of the test.
It turns out that such problems are very familiar to statisticians and
that the expected values of  needed to give different values
of the power at specified significance levels for a given df have
been tabulated extensively (see Pearson and Hartley, 1972).
The expected
needed to give different values
of the power at specified significance levels for a given df have
been tabulated extensively (see Pearson and Hartley, 1972).
The expected  is known as the
centrality parameter (
is known as the
centrality parameter (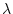 ) of
the non-central
) of
the non-central  distribution (i.e., when the null-hypothesis is false). Selected
values of the non-centrality parameter are given in
Table 7.1 for a
distribution (i.e., when the null-hypothesis is false). Selected
values of the non-centrality parameter are given in
Table 7.1 for a  test with 1 df and a
significance level of 0.05.
test with 1 df and a
significance level of 0.05.
Table 7.1:
Non-centrality parameter, 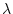 , of non-central
, of non-central
 distribution for 1 df required to give selected values of the
power of the test at the 5% significance level (selected from Pearson
and Hartley, 1972).
distribution for 1 df required to give selected values of the
power of the test at the 5% significance level (selected from Pearson
and Hartley, 1972).
| Desired Power |
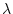 |
| 0.25 |
1.65 |
| 0.50 |
3.84 |
| 0.75 |
6.94 |
| 0.80 |
7.85 |
| 0.90 |
10.51 |
| 0.95 |
13.00 |
With 1000 pairs of MZ and DZ twins, we find a non-centrality parameter
of 11.35 when we use the  test to detect
test to detect 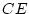 which explains
20% of the variation in our hypothetical population. This
corresponds to a power somewhere between 90% (
which explains
20% of the variation in our hypothetical population. This
corresponds to a power somewhere between 90% (
 ) and
95% (
) and
95% ( ). That is, 1000 pairs each of MZ and DZ twins
would allow us to detect, at the 5% significance level, a significant
shared environmental effect when the true value of
). That is, 1000 pairs each of MZ and DZ twins
would allow us to detect, at the 5% significance level, a significant
shared environmental effect when the true value of 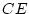 was 0.20 in
about 90-95% of all possible samples of this size and composition.
Conversely, we would only fail to detect this much shared environment
in about 5-10% of all possible studies.
Suppose now that we want to figure out the sample size needed to give
a power of 80%. Let this sample size be
was 0.20 in
about 90-95% of all possible samples of this size and composition.
Conversely, we would only fail to detect this much shared environment
in about 5-10% of all possible studies.
Suppose now that we want to figure out the sample size needed to give
a power of 80%. Let this sample size be 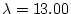 . Let
. Let  be the
sample size assumed in the initial power analysis (2000 pairs, in our
case). Let the expected
be the
sample size assumed in the initial power analysis (2000 pairs, in our
case). Let the expected  for the particular test being
explored with this sample size be
for the particular test being
explored with this sample size be  (11.35, in this example).
From Table 7.1, we see that the non-centrality
parameter,
(11.35, in this example).
From Table 7.1, we see that the non-centrality
parameter, 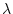 , needs to be 7.85 to give a power of 0.80. Since
the value of
, needs to be 7.85 to give a power of 0.80. Since
the value of  is expected to increase linearly as a function
of sample size we can obtain the sample size necessary to give 80%
power by solving:
is expected to increase linearly as a function
of sample size we can obtain the sample size necessary to give 80%
power by solving:
That is, in a sample comprising 50% MZ and 50% DZ pairs reared
together, we would require 1,383 pairs in total, or approximately 692
pairs of each type to be 80% certain of detecting a shared
environmental effect explaining 20% of the total variance, when a
further 30% is due to additive genetic factors.
It must be emphasized again that this particular sample size is
specific to the study design, sample structure, parameter values and
significance level assumed in the simulation. Smaller samples will be
needed to detect larger effects. Greater power requires larger
samples. Larger studies can detect smaller effects, and finally, some
parameters of the model may be easier to detect than others.




Next: 5 Loss of Power
Up: 7 Power and Sample
Previous: 3 Steps in Power
Index
Jeff Lessem
2002-03-21
![[*]](crossref.png) we show a version of the Mx code for
fitting the ACE model to the simulated covariance matrices. In
addition to the expected covariances we must assign an arbitrary
sample size and structure. Initially, we shall assume the study
involves equal numbers, 1000 each, of MZ and DZ pairs. In order to
conduct the power calculations for the
we show a version of the Mx code for
fitting the ACE model to the simulated covariance matrices. In
addition to the expected covariances we must assign an arbitrary
sample size and structure. Initially, we shall assume the study
involves equal numbers, 1000 each, of MZ and DZ pairs. In order to
conduct the power calculations for the