



Next: 3 Sibling Interaction Model
Up: 8 Social Interaction
Previous: 1 Introduction
Index
2 Basic Univariate Model without Interaction
Up to this point, we have been concerned primarily with decomposing
observed phenotypic variation into its genetic and environmental
components. This has been accomplished by estimating the paths from
latent or independent variables to dependent variables.
A basic univariate path diagram is set out in Figure 8.1.
Figure 8.1:
Basic path diagram for univariate twin data.
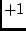 |
This path diagram shows the deviation phenotypes 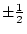 and
and 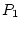 , of a pair of
twins. Here we refer to the phenotypes as deviation phenotypes
to emphasize the point that the
model assumes variables to be measured as deviations from the means, which is
the case whenever we fit models to covariance matrices and do not include
means. The deviation phenotypes
, of a pair of
twins. Here we refer to the phenotypes as deviation phenotypes
to emphasize the point that the
model assumes variables to be measured as deviations from the means, which is
the case whenever we fit models to covariance matrices and do not include
means. The deviation phenotypes 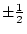 and
and 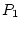 result from their respective
additive genetic deviations,
result from their respective
additive genetic deviations,  and
and  , their shared environment
deviations,
, their shared environment
deviations,  and
and 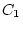 , and their non-shared environmental deviations,
, and their non-shared environmental deviations,
 and
and 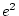 . The linear model corresponding to the path diagram is:
. The linear model corresponding to the path diagram is:
In matrix form we can write:
or as a matrix expression
Details of specifying and estimating this basic univariate model are
given in Chapter 6. One of the interesting assumptions of
this basic ACE model is that the siblings' or twins' phenotypes
have no influence on each other. This assumption may well be true of
height or finger print ridge count, but is it necessarily true for a
behavior like smoking, a psychiatric condition like depression,
delinquent behavior in children or even an anthropometric measure like
the body mass index? We should not, in general, assume a priori
that a source of variation is absent, especially when an empirical
test of the assumption may be readily performed. However, we may as
well recognize from the onset that evidence for social interactions or
sibling effects is pretty scarce. The fact is that usually one form
or another of the basic univariate model adequately describes a twin
or family data set, within the power of the study. This tells us that
there will not be evidence of significant social interactions since,
were such effects substantial, they would lead to failure of basic
univariate models. Nevertheless, this extension of the basic models
is of considerable theoretical interest and studying its outcome on
the expectations derived from the models can provide insight into the
nature and results of social influences. The applications to
bivariate and multivariate causal modeling are perhaps even more
intriguing and will be taken up in chapter ![[*]](crossref.png) .
.




Next: 3 Sibling Interaction Model
Up: 8 Social Interaction
Previous: 1 Introduction
Index
Jeff Lessem
2002-03-21
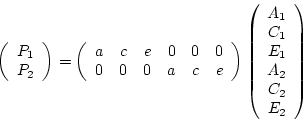
![[*]](crossref.png) .
.