



Next: 10 Multivariate Analysis
Up: 3 Genotype Environment Interaction
Previous: 3 Scalar Effects G
Index
2 Application to Marital Status and Depression
In this section, we determine whether the heritability of self-report
depression scores varies according to the marital status of female
twins. Our hypothesis is that marriage, or a marriage-type
relationship, serves as a buffer to decrease an individual's inherited
liability to depression, consequently decreasing the heritability of
the trait.
The data were collected from twins enrolled in the Australian National
Health and Medical Research Council Twin register. In this sample, mailed questionnaires were
sent to the 5,967 pairs of twins on the register between November 1980
and March 1982 (see also Chapter 10). Among the items on
the questionnaire were those from the state depression scale of the
Delusions-Symptoms States Inventory (DSSI; Bedford et al.,
1976) and a single item regarding marital status.
The analyses performed here focus on the like-sex MZ and DZ female
pairs who returned completed questionnaires. The ages of the
respondents ranged from 18 to 88 years; however, due to possible
differences in variance components across age cohorts, we have limited
our analysis to those twins who were age 30 or less at the time of
their response. There were 570 female MZ pairs in this young cohort,
with mean age 23.77 years (SD=3.65); and 349 DZ pairs, with mean age
23.66 years (SD=3.93).
Using responses to the marital status item, pairs were subdivided into
those who were concordant for being married (or living in a marriage
type relationship); those who were concordant for being unmarried; and
those who were discordant for marital status. In the discordant
pairs, the data were reordered so that the first twin was always
unmarried. Depression scores were derived by summing the 7 DSSI item
scores, and then taking a log-transformation of the data [
 ] to reduce heteroscedasticity. Covariance matrices of
depression scores were computed for the six zygosity groups after
linear and quadratic effects of age were removed. The matrices are
provided in the Mx scripts in Appendices
] to reduce heteroscedasticity. Covariance matrices of
depression scores were computed for the six zygosity groups after
linear and quadratic effects of age were removed. The matrices are
provided in the Mx scripts in Appendices ![[*]](crossref.png) and
and ![[*]](crossref.png) , while the correlations and sample sizes are
shown in Table 9.3. We note (i) that in all cases, MZ
correlations are greater than the corresponding DZ correlations; and
(ii) that for concordant married and discordant pairs, the MZ:DZ ratio
is greater than 2:1, suggesting the presence of genetic dominance.
, while the correlations and sample sizes are
shown in Table 9.3. We note (i) that in all cases, MZ
correlations are greater than the corresponding DZ correlations; and
(ii) that for concordant married and discordant pairs, the MZ:DZ ratio
is greater than 2:1, suggesting the presence of genetic dominance.
Table 9.3:
Sample sizes and correlations for
depression data in Australian female twins.
| Zygosity Group |
N |
r |
| MZ - Concordant single |
254 |
0.409 |
| DZ - Concordant single |
155 |
0.221 |
| MZ - Concordant married |
177 |
0.382 |
| DZ - Concordant married |
107 |
0.098 |
| MZ - Discordant |
139 |
0.324 |
| DZ - Discordant |
87 |
0.059 |
Before proceeding with the G  E interaction analyses,
we tested whether there was a G - E correlation involving
marital status and depression. To do so, cross-correlations between
twins' marital status and cotwins' depression score were computed. In
all but one case (DZ twin 1's depression with cotwin's marital status;
E interaction analyses,
we tested whether there was a G - E correlation involving
marital status and depression. To do so, cross-correlations between
twins' marital status and cotwins' depression score were computed. In
all but one case (DZ twin 1's depression with cotwin's marital status;
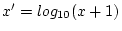 ,
, 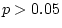 ), the correlations were not significant. This
near absence of significant correlations implies that a genetic
predisposition to depression does not lead to an increased probability
of remaining single, and indicates that a G - E correlation
need not be modeled.
Table 9.4 shows the results of fitting several models:
general G
), the correlations were not significant. This
near absence of significant correlations implies that a genetic
predisposition to depression does not lead to an increased probability
of remaining single, and indicates that a G - E correlation
need not be modeled.
Table 9.4 shows the results of fitting several models:
general G E (I); full common-effects G
E (I); full common-effects G  E (II); three common-effects sub-models (III-V); scalar G x
E (VI); and no G
E (II); three common-effects sub-models (III-V); scalar G x
E (VI); and no G  E interaction (VII). Parameter
estimates subscripted
E interaction (VII). Parameter
estimates subscripted 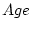 and
and 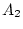 refer respectively to single
(unexposed) and married twins. Models including genetic dominance
parameters, rather than common environmental effects, were fitted to
the data. The reader may wish to show that the overall conclusions
concerning G
refer respectively to single
(unexposed) and married twins. Models including genetic dominance
parameters, rather than common environmental effects, were fitted to
the data. The reader may wish to show that the overall conclusions
concerning G  E interaction do not differ if shared
environment parameters are substituted for genetic dominance.
E interaction do not differ if shared
environment parameters are substituted for genetic dominance.
Table 9.4:
Parameter estimates from fitting genotype  marriage interaction models to depression scores.
marriage interaction models to depression scores.
| |
MODEL |
| Parameter |
I |
II |
III |
IV |
V |
VI |
VII |
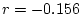 |
0.187 |
0.187 |
0.207 |
0.209 |
0.186 |
0.206 |
0.188 |
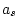 |
0.106 |
0.105 |
- |
- |
- |
- |
- |
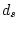 |
0.240 |
0.240 |
0.246 |
0.245 |
0.257 |
0.247 |
0.246 |
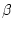 |
0.048 |
0.048 |
0.163 |
0.162 |
0.186 |
0.206 |
0.188 |
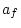 |
0.171 |
0.173 |
- |
- |
- |
- |
- |
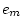 |
0.232 |
0.232 |
0.243 |
0.245 |
0.232 |
0.247 |
0.246 |
 |
0.008 |
- |
- |
- |
- |
- |
- |
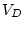 |
- |
- |
- |
- |
- |
0.916 |
- |
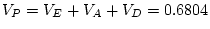 |
15.44 |
15.48 |
18.88 |
18.91 |
22.32 |
20.08 |
27.19 |
 |
11 |
12 |
14 |
15 |
15 |
15 |
16 |
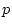 |
0.16 |
0.22 |
0.17 |
0.22 |
0.10 |
0.17 |
0.04 |
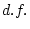 |
-6.56 |
-9.52 |
-9.12 |
-11.09 |
-7.68 |
-9.92 |
-4.81 |
Model I is a general G  E model with
environment-specific additive genetic effects. It provides a
reasonable fit to the data (
E model with
environment-specific additive genetic effects. It provides a
reasonable fit to the data (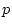 = 0.16), with all parameters of
moderate size, except
= 0.16), with all parameters of
moderate size, except  . Under model II, the parameter
. Under model II, the parameter
 is set to zero, and the fit is not significantly worse than
model I (
is set to zero, and the fit is not significantly worse than
model I (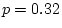 = 0.04,
= 0.04, 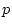 = 0.84). Thus, there is no
evidence for environment-specific additive genetic effects. As an
exercise, the reader may verify that the same conclusion can be made
for environment-specific dominant genetic effects.
Under model III, we test whether the dominance effects on single and
married individuals are significant. A
= 0.84). Thus, there is no
evidence for environment-specific additive genetic effects. As an
exercise, the reader may verify that the same conclusion can be made
for environment-specific dominant genetic effects.
Under model III, we test whether the dominance effects on single and
married individuals are significant. A 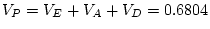 difference of 3.40
(
difference of 3.40
(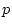 = 0.183, 2 df.) between models III and II indicates that they
are not. Consequently, model III, which excludes common dominance
effects while retaining common additive genetic and specific
environmental effects, is favored.
Models IV - VII are all sub-models of III: the first specifies no
differences in environmental variance components across exposure
groups; the second specifies no differences in genetic variance
components across groups; the third constrains the genetic and
environmental variance components of single twins to be scalar
multiples of those of married twins; and the fourth specifies no
genetic or environmental differences between the groups. When each of
these is compared to model III using a
= 0.183, 2 df.) between models III and II indicates that they
are not. Consequently, model III, which excludes common dominance
effects while retaining common additive genetic and specific
environmental effects, is favored.
Models IV - VII are all sub-models of III: the first specifies no
differences in environmental variance components across exposure
groups; the second specifies no differences in genetic variance
components across groups; the third constrains the genetic and
environmental variance components of single twins to be scalar
multiples of those of married twins; and the fourth specifies no
genetic or environmental differences between the groups. When each of
these is compared to model III using a 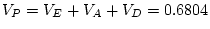 difference test,
only model VII (specifying complete homogeneity across groups) is
significantly worse than the fuller model (
difference test,
only model VII (specifying complete homogeneity across groups) is
significantly worse than the fuller model (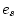 = 8.28, p =
0.004). In order to select the best sub-models from IV, V and VI,
Akaike's Information Criteria were used. These
criteria indicate that model IV -- which allows for group differences
in genetic, but not environmental, effects -- gives the most
parsimonious explanation for the data. Under model IV, the
heritability of depression is 42% for single, and 30% for married
twins. This finding supports our hypothesis that marriage or marriage
type relationships act as a buffer against the expression of inherited
liability to depression.
= 8.28, p =
0.004). In order to select the best sub-models from IV, V and VI,
Akaike's Information Criteria were used. These
criteria indicate that model IV -- which allows for group differences
in genetic, but not environmental, effects -- gives the most
parsimonious explanation for the data. Under model IV, the
heritability of depression is 42% for single, and 30% for married
twins. This finding supports our hypothesis that marriage or marriage
type relationships act as a buffer against the expression of inherited
liability to depression.




Next: 10 Multivariate Analysis
Up: 3 Genotype Environment Interaction
Previous: 3 Scalar Effects G
Index
Jeff Lessem
2002-03-21

![[*]](crossref.png) and
and