



Next: 2 Psychometric Model
Up: 2 Models for Multiple
Previous: 2 Models for Multiple
Index
1 Rater Bias Model
Figure 11.1 shows a path model for the ratings of twins by their
Figure 11.1:
Model for ratings of a pair of twins (1 and 2) by their parents.
Maternal and paternal
observed ratings ( and
and 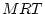 ) are linear functions of the true phenotypes of
the twins (
) are linear functions of the true phenotypes of
the twins (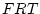 ), maternal and paternal rater bias (
), maternal and paternal rater bias (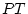 and
and 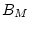 ), and
residual error (
), and
residual error (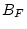 and
and 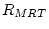 ).
).
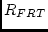 |
parents, in which the phenotypes of a pair of twins (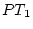 and
and
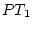 ) are functions of additive genetic influence (
) are functions of additive genetic influence (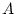 ), shared
environments (
), shared
environments (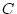 ) and non-shared environments (
) and non-shared environments (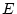 ). The ratings by the
mother (
). The ratings by the
mother ( ) and father (
) and father (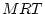 ) are functions of the twin's phenotype,
the maternal (
) are functions of the twin's phenotype,
the maternal (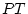 ) or paternal (
) or paternal (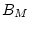 ) rater bias, and residual
errors (
) rater bias, and residual
errors (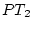 , etc).
If this model is correct, the following discriminations may be made:
, etc).
If this model is correct, the following discriminations may be made:
- the structural analysis of the latent phenotypes of the children
can be considered independently of the rater biases and
unreliability of the ratings;
- the extent of rater biases and unreliability of ratings can be
estimated;
- the relative accuracy of maternal and paternal ratings can be
assessed.
A simple implementation of the model in Mx is achieved by defining the
model by the following matrix equations:
 |
|
|
(68) |
or
and
or
Thus
Then, the covariance matrix of the ratings is given by
The term
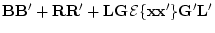 generates the usual
expectations for the ACE model. The expectations are filtered to the
observed ratings through the factor structure L and are augmented by
the contributions from rater bias (
generates the usual
expectations for the ACE model. The expectations are filtered to the
observed ratings through the factor structure L and are augmented by
the contributions from rater bias (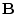 ) and residual influences
(
) and residual influences
(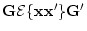 ). An Mx script for this model is listed in
Appendix
). An Mx script for this model is listed in
Appendix ![[*]](crossref.png) . In considering the rater bias model, and
the other models discussed below, we should note that parameters need
not be constrained to be equal when rating boys and girls and, as
Neale and Stevenson (1988) pointed out, we
need not necessarily assume that parental biases are equal for MZ and
DZ twins' ratings. This latter relaxation of the parameter
constraints allows us to consider the possibility that twin
correlations differ across zygosities for reasons related to
differential parental biases based on beliefs about their twins'
zygosity.
. In considering the rater bias model, and
the other models discussed below, we should note that parameters need
not be constrained to be equal when rating boys and girls and, as
Neale and Stevenson (1988) pointed out, we
need not necessarily assume that parental biases are equal for MZ and
DZ twins' ratings. This latter relaxation of the parameter
constraints allows us to consider the possibility that twin
correlations differ across zygosities for reasons related to
differential parental biases based on beliefs about their twins'
zygosity.




Next: 2 Psychometric Model
Up: 2 Models for Multiple
Previous: 2 Models for Multiple
Index
Jeff Lessem
2002-03-21

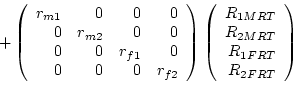
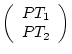
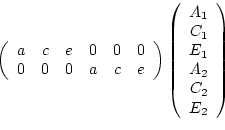
![[*]](crossref.png) . In considering the rater bias model, and
the other models discussed below, we should note that parameters need
not be constrained to be equal when rating boys and girls and, as
Neale and Stevenson (1988) pointed out, we
need not necessarily assume that parental biases are equal for MZ and
DZ twins' ratings. This latter relaxation of the parameter
constraints allows us to consider the possibility that twin
correlations differ across zygosities for reasons related to
differential parental biases based on beliefs about their twins'
zygosity.
. In considering the rater bias model, and
the other models discussed below, we should note that parameters need
not be constrained to be equal when rating boys and girls and, as
Neale and Stevenson (1988) pointed out, we
need not necessarily assume that parental biases are equal for MZ and
DZ twins' ratings. This latter relaxation of the parameter
constraints allows us to consider the possibility that twin
correlations differ across zygosities for reasons related to
differential parental biases based on beliefs about their twins'
zygosity.