



Next: 3 Biometric Model
Up: 2 Models for Multiple
Previous: 1 Rater Bias Model
Index
2 Psychometric Model
Figure 11.2 shows a bivariate psychometric or `common
pathway' model. Implementation of this
model in Mx can be achieved by the
Figure 11.2:
Psychometric or common pathway model for ratings of a pair of
twins (1 and 2) by their parents. Maternal and paternal observed
ratings ( and
and 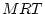 ) are linear functions of the latent phenotypes of
the twins (
) are linear functions of the latent phenotypes of
the twins (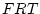 ), and rater specific variance (e.g.,
), and rater specific variance (e.g., 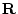 ,
, 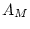 and
and 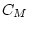 ).
).
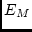 |
approaches illustrated in Chapter 10. The psychometric
model estimates, for each source of influence (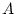 ,
, 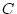 , and
, and 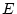 ) the
variance for mothers' ratings, the variance for fathers' ratings and
the covariance between these ratings. These estimates are subject to
the constraints that the covariances are positive and neither
individual rating variance can be less than the covariance between the
ratings. The psychological implication of this psychometric model is
that the mothers' and fathers' ratings are composed of consistent
assessments of reliable trait variance, together with assessments of
specific phenotypes uncorrelated between the parents.
There are some technical points to note with this model. First,
bivariate data for MZ and DZ twins (of a given sex) yield 20 observed
variances and covariances. However, only 9 of these have unique
expectations under the classes of model we are considering, the
remaining 11 being replicate estimates of particular expectations
(e.g., the variance of maternal ratings of MZ twin 1, of MZ twin 2, of
DZ twin 1 and of DZ twin 2 are four replicate estimates of the
variance of maternal ratings in the population). Given this, we might
expect our 9 parameter psychometric model to fit as well as any other
9 parameter model for bivariate twin data. However, there are some
implicit constraints in our psychometric model. For example, the
phenotypic covariance of mothers' and fathers' ratings cannot be
greater than the variance of either type of rating. Such constraints
may cause the model to fail in some circumstances even though the 9
parameter biometric model discussed below (Figure 11.3) may
fit adequately
) the
variance for mothers' ratings, the variance for fathers' ratings and
the covariance between these ratings. These estimates are subject to
the constraints that the covariances are positive and neither
individual rating variance can be less than the covariance between the
ratings. The psychological implication of this psychometric model is
that the mothers' and fathers' ratings are composed of consistent
assessments of reliable trait variance, together with assessments of
specific phenotypes uncorrelated between the parents.
There are some technical points to note with this model. First,
bivariate data for MZ and DZ twins (of a given sex) yield 20 observed
variances and covariances. However, only 9 of these have unique
expectations under the classes of model we are considering, the
remaining 11 being replicate estimates of particular expectations
(e.g., the variance of maternal ratings of MZ twin 1, of MZ twin 2, of
DZ twin 1 and of DZ twin 2 are four replicate estimates of the
variance of maternal ratings in the population). Given this, we might
expect our 9 parameter psychometric model to fit as well as any other
9 parameter model for bivariate twin data. However, there are some
implicit constraints in our psychometric model. For example, the
phenotypic covariance of mothers' and fathers' ratings cannot be
greater than the variance of either type of rating. Such constraints
may cause the model to fail in some circumstances even though the 9
parameter biometric model discussed below (Figure 11.3) may
fit adequately![[*]](footnote.png) . The second technical point is
that if we do not constrain the loadings of the common factor to be
equal on the mothers' ratings and on the fathers' ratings, and assume
that there is no specific genetic variance for either mothers' ratings
or for fathers' ratings, then this variant of the psychometric model
is formally equivalent to our version in the Neale and Stevenson bias model described above. In this case
the ``shared environmental'' specific variances for the mothers' and
fathers' ratings are formally equivalent to the maternal and paternal
biases in the earlier model, while the ``non-shared'' specific
variances are equal to the unreliability variance of the earlier
parameterization. Thus, although the 9 parameter psychometric model
and the bias model do not form a nested pair (Mulaik et al.,
1989), they represent alternative sets of constraints on a more
general 10 parameter model (which is not identified with two-rater
twin data) and these constrained models may be compared in terms of
parsimony and goodness of fit. Furthermore, we may consider a
restricted bias model in which the scaling factor in
Figure 11.1 is set to unity and which, therefore, has 7
free parameters and is nested within both the psychometric model and
the unrestricted bias model. This restricted bias model may therefore
be tested directly against either the psychometric or the unrestricted
bias models by a likelihood ratio chi-square.
. The second technical point is
that if we do not constrain the loadings of the common factor to be
equal on the mothers' ratings and on the fathers' ratings, and assume
that there is no specific genetic variance for either mothers' ratings
or for fathers' ratings, then this variant of the psychometric model
is formally equivalent to our version in the Neale and Stevenson bias model described above. In this case
the ``shared environmental'' specific variances for the mothers' and
fathers' ratings are formally equivalent to the maternal and paternal
biases in the earlier model, while the ``non-shared'' specific
variances are equal to the unreliability variance of the earlier
parameterization. Thus, although the 9 parameter psychometric model
and the bias model do not form a nested pair (Mulaik et al.,
1989), they represent alternative sets of constraints on a more
general 10 parameter model (which is not identified with two-rater
twin data) and these constrained models may be compared in terms of
parsimony and goodness of fit. Furthermore, we may consider a
restricted bias model in which the scaling factor in
Figure 11.1 is set to unity and which, therefore, has 7
free parameters and is nested within both the psychometric model and
the unrestricted bias model. This restricted bias model may therefore
be tested directly against either the psychometric or the unrestricted
bias models by a likelihood ratio chi-square.




Next: 3 Biometric Model
Up: 2 Models for Multiple
Previous: 1 Rater Bias Model
Index
Jeff Lessem
2002-03-21
![[*]](footnote.png) . The second technical point is
that if we do not constrain the loadings of the common factor to be
equal on the mothers' ratings and on the fathers' ratings, and assume
that there is no specific genetic variance for either mothers' ratings
or for fathers' ratings, then this variant of the psychometric model
is formally equivalent to our version in the Neale and Stevenson bias model described above. In this case
the ``shared environmental'' specific variances for the mothers' and
fathers' ratings are formally equivalent to the maternal and paternal
biases in the earlier model, while the ``non-shared'' specific
variances are equal to the unreliability variance of the earlier
parameterization. Thus, although the 9 parameter psychometric model
and the bias model do not form a nested pair (Mulaik et al.,
1989), they represent alternative sets of constraints on a more
general 10 parameter model (which is not identified with two-rater
twin data) and these constrained models may be compared in terms of
parsimony and goodness of fit. Furthermore, we may consider a
restricted bias model in which the scaling factor in
Figure 11.1 is set to unity and which, therefore, has 7
free parameters and is nested within both the psychometric model and
the unrestricted bias model. This restricted bias model may therefore
be tested directly against either the psychometric or the unrestricted
bias models by a likelihood ratio chi-square.
. The second technical point is
that if we do not constrain the loadings of the common factor to be
equal on the mothers' ratings and on the fathers' ratings, and assume
that there is no specific genetic variance for either mothers' ratings
or for fathers' ratings, then this variant of the psychometric model
is formally equivalent to our version in the Neale and Stevenson bias model described above. In this case
the ``shared environmental'' specific variances for the mothers' and
fathers' ratings are formally equivalent to the maternal and paternal
biases in the earlier model, while the ``non-shared'' specific
variances are equal to the unreliability variance of the earlier
parameterization. Thus, although the 9 parameter psychometric model
and the bias model do not form a nested pair (Mulaik et al.,
1989), they represent alternative sets of constraints on a more
general 10 parameter model (which is not identified with two-rater
twin data) and these constrained models may be compared in terms of
parsimony and goodness of fit. Furthermore, we may consider a
restricted bias model in which the scaling factor in
Figure 11.1 is set to unity and which, therefore, has 7
free parameters and is nested within both the psychometric model and
the unrestricted bias model. This restricted bias model may therefore
be tested directly against either the psychometric or the unrestricted
bias models by a likelihood ratio chi-square.