



Next: 4 Comparison of Models
Up: 2 Models for Multiple
Previous: 2 Psychometric Model
Index
3 Biometric Model
The final model to be considered is the biometric model shown in
Figure 11.3, and
Figure 11.3:
Biometric or independent pathway model for
ratings of a pair of twins (1 and 2) by their parents. Maternal and
paternal observed ratings ( and
and 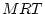 ) are linear functions of
general (subscript
) are linear functions of
general (subscript 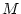 ) and restricted (subscript
) and restricted (subscript 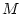 ) genetic and
environmental factors.
) genetic and
environmental factors.
 |
again may be readily implemented using the procedure described in
Chapter 10. In this model there are two factors for each
source of variance (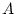 ,
, 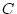 , and
, and 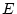 ). One factor is subscripted M, e.g.,
). One factor is subscripted M, e.g.,
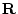 , and loads on the maternal rating (
, and loads on the maternal rating ( ) and on the paternal
rating (
) and on the paternal
rating (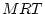 ). The other factor subscripted F, e.g.,
). The other factor subscripted F, e.g., 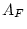 , loads only
on the paternal rating. Thus, for each source of influence we
estimate three factor loadings which enable us to reconstruct
estimates of the contribution of this influence to the variance of
maternal ratings, the variance of paternal ratings and the covariance
between them. Which factor loads on both types of rating and which on
only one is arbitrary. This type of model is referred to as a
Cholesky model or decomposition or a
triangular model and provides a standard general approach to
multivariate biometrical analysis (see Chapter 10). This
biometric model is a saturated unconstrained model for the nine unique
expected variances and covariances (in the absence of sibling
interactions or other influences giving rise to heterogeneity of
variances across zygosities, cf. Heath et
al., 1989) and provides the most general approach to estimating the
genetic, shared environmental and non-shared environmental components
of variance and covariance. However, the absence of theoretically
motivated constraints lessens the psychological informativeness of the
model for the analysis of parental ratings. In this context, we may
use the biometric model first to test the adequacy of the assumption
that of the 20 observed variances and covariances for bivariate twin
data of a given sex, 11 represent replicate estimates of the 9 unique
structural expectations. Once again, sex differences in factor
loadings (scalar sex limitation) may in principle lead to model
failure for opposite sex data even though the biometric model is
adequate for a given sex. In this case the non-scalar sex limitation
model described in Heath et al. (1989)
and Chapter 9 would be required. The bivariate biometric
model provides a baseline for comparison of the adequacy of the
psychometric and bias models. This comparison alerts us to the
important possibility that mothers and fathers are assessing different
(but possibly correlated) phenotypes as, for example, they might be if
mothers and fathers were reporting on behaviors observed in different
situations or without a common understanding of the behavioral
descriptions used in the assessment protocol.
, loads only
on the paternal rating. Thus, for each source of influence we
estimate three factor loadings which enable us to reconstruct
estimates of the contribution of this influence to the variance of
maternal ratings, the variance of paternal ratings and the covariance
between them. Which factor loads on both types of rating and which on
only one is arbitrary. This type of model is referred to as a
Cholesky model or decomposition or a
triangular model and provides a standard general approach to
multivariate biometrical analysis (see Chapter 10). This
biometric model is a saturated unconstrained model for the nine unique
expected variances and covariances (in the absence of sibling
interactions or other influences giving rise to heterogeneity of
variances across zygosities, cf. Heath et
al., 1989) and provides the most general approach to estimating the
genetic, shared environmental and non-shared environmental components
of variance and covariance. However, the absence of theoretically
motivated constraints lessens the psychological informativeness of the
model for the analysis of parental ratings. In this context, we may
use the biometric model first to test the adequacy of the assumption
that of the 20 observed variances and covariances for bivariate twin
data of a given sex, 11 represent replicate estimates of the 9 unique
structural expectations. Once again, sex differences in factor
loadings (scalar sex limitation) may in principle lead to model
failure for opposite sex data even though the biometric model is
adequate for a given sex. In this case the non-scalar sex limitation
model described in Heath et al. (1989)
and Chapter 9 would be required. The bivariate biometric
model provides a baseline for comparison of the adequacy of the
psychometric and bias models. This comparison alerts us to the
important possibility that mothers and fathers are assessing different
(but possibly correlated) phenotypes as, for example, they might be if
mothers and fathers were reporting on behaviors observed in different
situations or without a common understanding of the behavioral
descriptions used in the assessment protocol.




Next: 4 Comparison of Models
Up: 2 Models for Multiple
Previous: 2 Psychometric Model
Index
Jeff Lessem
2002-03-21