



Next: 2 Bivariate Normal Distribution
Up: 3 Ordinal Data Analysis
Previous: 3 Ordinal Data Analysis
Index
1 Univariate Normal Distribution of Liability
One approach to the analysis of ordinal data is to assume that the ordered
categories reflect imprecise measurement of an underlying normal distribution
of liability. A second assumption is that the liability distribution has
one or more threshold values
that discriminate between the categories (see
Figure 2.1). This model has been used widely in genetic applications
(Falconer, 1960; Neale et al., 1986; Neale, 1988;
Heath et al 1989a). As long as we consider one variable at a time, it is
Figure 2.1:
Univariate normal
distribution with thresholds distinguishing ordered response
categories.
 |
always possible to place the thresholds so that the proportion of the
distribution lying between adjacent thresholds exactly matches the
observed proportion of the sample that is found in each category. For
example, suppose we had an item with four possible responses:
`none', `a little', `quite a lot', and `a great deal'. In a sample of 200
subjects, 20 say `none', 80 say `a little', 98 say `quite a lot' and 2
say `a great deal'. If our assumed underlying normal distribution has mean 0
and variance 1, then placing thresholds at z-values of -1.282, 0.0 and
2.326 would partition the normal distribution as required. In
mathematical terms, if there are 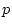 categories,
categories,
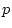 thresholds are needed to divide the distribution. The expected
proportion lying in category
thresholds are needed to divide the distribution. The expected
proportion lying in category 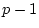 is
is
where  ,
, 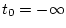 , and
, and 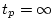 is the unit variance normal probability
density function (pdf), given by
is the unit variance normal probability
density function (pdf), given by
This formulation is really a parametric model for the distribution
of ordinal responses.




Next: 2 Bivariate Normal Distribution
Up: 3 Ordinal Data Analysis
Previous: 3 Ordinal Data Analysis
Index
Jeff Lessem
2002-03-21