



Next: 3 Testing the Normal
Up: 3 Ordinal Data Analysis
Previous: 1 Univariate Normal Distribution
Index
2 Bivariate Normal Distribution of Liability
When we have only one variable, there is no goodness-of-fit test for the
liability model because it always gives a perfect fit. However, this is not
necessarily so when we move to the multivariate case. Consider
first, the example where we have two variables, each measured as a simple
`yes/no' binary response. Data collected from a sample of subjects
could be summarized as a contingency table:
| |
Item 1 |
| Item 2 |
No |
Yes |
| Yes |
13 |
55 |
| No |
32 |
15 |
It is at this point that we encounter the crucial statistical concept
of degrees of freedom (df). Fortunately,
though important, calculating the
number of df for a model is usually very easy; it is simply the difference
between the number of observed statistics
and the number of parameters in the
model. In the present case we have a  contingency table in which
there are four observed frequencies. However, if we take the total sample size
as given and work with the proportion of the sample observed in each cell, we
only need three proportions to describe the table completely, because the total
of the cell proportions is 1 and the last cell proportion always can be
obtained by subtraction. Thus in general for a table with
contingency table in which
there are four observed frequencies. However, if we take the total sample size
as given and work with the proportion of the sample observed in each cell, we
only need three proportions to describe the table completely, because the total
of the cell proportions is 1 and the last cell proportion always can be
obtained by subtraction. Thus in general for a table with  rows and
rows and 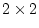 columns we can describe the data as
columns we can describe the data as 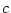 frequencies or as
frequencies or as 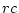 proportions
and the total sample size. The next question is, how many parameters does our
model contain?
The natural extension of the univariate normal liability model described above is to
assume that there is a continuous, bivariate normal distribution underlying the
distribution of our observations. Given this model, we can compute the expected
proportions for the four cells of the contingency table
proportions
and the total sample size. The next question is, how many parameters does our
model contain?
The natural extension of the univariate normal liability model described above is to
assume that there is a continuous, bivariate normal distribution underlying the
distribution of our observations. Given this model, we can compute the expected
proportions for the four cells of the contingency table![[*]](footnote.png) . The model is
illustrated graphically as contour and 3-D plots in Figure 2.2.
. The model is
illustrated graphically as contour and 3-D plots in Figure 2.2.
Figure 2.2:
Contour and 3-D plots of the bivariate normal
distribution with thresholds distinguishing two response
categories. Contour plot in top left shows zero correlation in
liability and plot in bottom left shows
correlation of .9; the panels on the right shows the same data as 3-D plots.
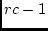 |
The figures contrast the uncorrelated case ( ) with a high
correlation in liability (
) with a high
correlation in liability (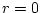 ) and are dramatically similar to
the
scatterplots of data from unrelated persons and from MZ twins, shown
in Figures 1.2 and 1.4 on
pages
) and are dramatically similar to
the
scatterplots of data from unrelated persons and from MZ twins, shown
in Figures 1.2 and 1.4 on
pages ![[*]](crossref.png) and
and ![[*]](crossref.png) . By adjusting the
correlation in liability and the two thresholds, the model can predict
any combination of proportions in the four cells. Because we use 3
parameters to predict the 3 observed proportions, there are no
degrees of freedom to test the goodness of fit of the model. This can
be seen when we consider an arbitrary non-normal distribution created
by mixing two normal distributions, one with
. By adjusting the
correlation in liability and the two thresholds, the model can predict
any combination of proportions in the four cells. Because we use 3
parameters to predict the 3 observed proportions, there are no
degrees of freedom to test the goodness of fit of the model. This can
be seen when we consider an arbitrary non-normal distribution created
by mixing two normal distributions, one with 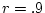 and the second
with
and the second
with 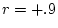 , as shown in Figure 2.3. With thresholds imposed
as shown, equal
, as shown in Figure 2.3. With thresholds imposed
as shown, equal
Figure 2.3:
Contour plots of a bivariate normal distribution with correlation
.9 (top); and of a mixture of bivariate normal distributions (bottom), one with .9
correlation and the other with -.9 correlation. One threshold in each
dimension is shown.
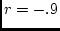 |
proportions are expected in each cell, corresponding to a zero
correlation and zero thresholds, not an unreasonable result but
with just two categories we have no knowledge at all that our
distribution is such a bizarre non-normal example. The case of a  contingency table is really a
`worst case scenario' for no degrees of freedom associated with a model, since
absolutely any pattern of observed frequencies could be accounted for with the
liability model. Effectively, all the model does is to transform the data; it
cannot be falsified.
contingency table is really a
`worst case scenario' for no degrees of freedom associated with a model, since
absolutely any pattern of observed frequencies could be accounted for with the
liability model. Effectively, all the model does is to transform the data; it
cannot be falsified.




Next: 3 Testing the Normal
Up: 3 Ordinal Data Analysis
Previous: 1 Univariate Normal Distribution
Index
Jeff Lessem
2002-03-21
 rows and
rows and ![[*]](footnote.png) . The model is
illustrated graphically as contour and 3-D plots in Figure 2.2.
. The model is
illustrated graphically as contour and 3-D plots in Figure 2.2.
![[*]](crossref.png) and
and ![[*]](crossref.png) . By adjusting the
correlation in liability and the two thresholds, the model can predict
any combination of proportions in the four cells. Because we use 3
parameters to predict the 3 observed proportions, there are no
degrees of freedom to test the goodness of fit of the model. This can
be seen when we consider an arbitrary non-normal distribution created
by mixing two normal distributions, one with
. By adjusting the
correlation in liability and the two thresholds, the model can predict
any combination of proportions in the four cells. Because we use 3
parameters to predict the 3 observed proportions, there are no
degrees of freedom to test the goodness of fit of the model. This can
be seen when we consider an arbitrary non-normal distribution created
by mixing two normal distributions, one with