



Next: 4 Model for Age-Correction
Up: 3 Fitting Genetic Models
Previous: 3 Fitting Genetic Models
Index
1 Major Depressive Disorder in Twins
Data for this example come from a study of genetic and environmental
risk factors for common psychiatric disorders in Caucasian female
same-sex twin pairs sampled from the Virginia Twin Registry. The
Virginia Twin Registry is a population-based register formed from a
systematic review of all birth certificates in the Commonwealth of
Virginia. Twins were eligible to participate in the study if they
were born between 1934 and 1971 and if both members of the pair had
previously responded to a mailed questionnaire, to which the
individual response rate was approximately 64%. The cooperation rate
was almost certainly higher than this, as an unknown number of twins
did not receive their questionnaire due to faulty addresses, improper
forwarding of mail, and so on. Of the total 1176 eligible pairs,
neither twin was interviewed in 46, one twin was interviewed and the
other refused in 97, and both twins were interviewed in 1033 pairs.
Of the completed interviews, 89.3% were completed face to face,
nearly all in the twins' home, and 10.7% (mostly twins living outside
Virginia) were interviewed by telephone. The mean age (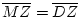 SD) of
the sample at interview was 30.1 (7.6) and ranged from 17 to 55.
Zygosity determination was based on a
combination of review of responses to questions about physical
similarity and frequency of confusion as children -- which alone have
proved capable of determining zygosity with over 95% accuracy
(Eaves et al., 1989b) --
and, in over 80% of cases, photographs of both twins. From this
information, twins were classified as either: definitely MZ,
definitely DZ, probably MZ, probably DZ, or uncertain. For 118 of the
186 pairs in the final three categories, blood was taken and eight
highly informative DNA polymorphisms were used to resolve zygosity.
If all probes are identical then there is a .9997 probability that the
pair is MZ (Spence et al., 1988). Final
zygosity determination, using blood samples where available, yielded
590 MZ pairs, 440 DZ pairs and 3 pairs classified as uncertain. The
DNA methods validated the questionnaire- and photograph-based
`probable' diagnoses in 84 out of 104 pairs; all 26 of 26 pairs in the
definite categories were confirmed as having an accurate diagnosis.
The error rate in zygosity assignment is probably well under 2%.
Lifetime psychiatric illness was diagnosed using an adapted version of
the Structured Clinical Interview for DSM-III-R Diagnosis
(Spitzer et al., 1987) an instrument with
demonstrable reliability in the diagnosis of depression (Riskind
et al., 1987). Interviewers were initially
trained for 80 hours and received bimonthly review sessions during the
course of the study. Each member of a twin pair was invariably
interviewed by a different interviewer. DSM-III-R criteria were
applied by a blind review of the interview by K.S.
Kendler, an experienced psychiatric
diagnostician. Diagnosis of depression was not given when the
symptoms were judged to be the result of uncomplicated bereavement,
medical illness, or medication. Inter-rater reliability was assessed
in 53 jointly conducted interviews. Chance corrected agreement
(kappa) was .96, though this is likely to be a substantial
overestimate of the value that would be obtained from independent
assessments
SD) of
the sample at interview was 30.1 (7.6) and ranged from 17 to 55.
Zygosity determination was based on a
combination of review of responses to questions about physical
similarity and frequency of confusion as children -- which alone have
proved capable of determining zygosity with over 95% accuracy
(Eaves et al., 1989b) --
and, in over 80% of cases, photographs of both twins. From this
information, twins were classified as either: definitely MZ,
definitely DZ, probably MZ, probably DZ, or uncertain. For 118 of the
186 pairs in the final three categories, blood was taken and eight
highly informative DNA polymorphisms were used to resolve zygosity.
If all probes are identical then there is a .9997 probability that the
pair is MZ (Spence et al., 1988). Final
zygosity determination, using blood samples where available, yielded
590 MZ pairs, 440 DZ pairs and 3 pairs classified as uncertain. The
DNA methods validated the questionnaire- and photograph-based
`probable' diagnoses in 84 out of 104 pairs; all 26 of 26 pairs in the
definite categories were confirmed as having an accurate diagnosis.
The error rate in zygosity assignment is probably well under 2%.
Lifetime psychiatric illness was diagnosed using an adapted version of
the Structured Clinical Interview for DSM-III-R Diagnosis
(Spitzer et al., 1987) an instrument with
demonstrable reliability in the diagnosis of depression (Riskind
et al., 1987). Interviewers were initially
trained for 80 hours and received bimonthly review sessions during the
course of the study. Each member of a twin pair was invariably
interviewed by a different interviewer. DSM-III-R criteria were
applied by a blind review of the interview by K.S.
Kendler, an experienced psychiatric
diagnostician. Diagnosis of depression was not given when the
symptoms were judged to be the result of uncomplicated bereavement,
medical illness, or medication. Inter-rater reliability was assessed
in 53 jointly conducted interviews. Chance corrected agreement
(kappa) was .96, though this is likely to be a substantial
overestimate of the value that would be obtained from independent
assessments![[*]](footnote.png) .
Contingency tables of MZ and DZ twin pair diagnoses are shown in
Table 6.9.
.
Contingency tables of MZ and DZ twin pair diagnoses are shown in
Table 6.9.
Table 6.9:
Contingency tables of twin pair diagnosis of lifetime Major Depressive
Disorder in Virginia adult female twins.
| |
|
MZ |
DZ |
| |
Twin 1 |
Normal |
Depressed |
Normal |
Depressed |
| Twin 2 |
Normal |
329 |
83 |
201 |
94 |
| |
Depressed |
95 |
83 |
82 |
63 |
PRELIS estimates of the correlation in liability to depression are
.435 for MZ and .186 for DZ pairs. Details of using PRELIS to derive
these statistics and associated estimates of their asymptotic
variances are given in Section 2.3.
The PMatrix command is used to read in the tetrachoric
correlation matrix, and the ACov command reads the asymptotic
weight matrices. In both cases we use the File= keyword in
order to read these data from files. Therefore our univariate Mx
input script is unchanged from that shown in Appendix ![[*]](crossref.png) on page
on page ![[*]](crossref.png) , except for the title and the dat file used.
, except for the title and the dat file used.
Major depressive disorder in adult female MZ twins
Data NInput_vars=2 NObservations=590
#Include mzdepsum.dat
where the dat file reads
PMatrix File=MZdep.cov
ACov File=MZdep.asy
in the MZ group, with the same commands for the DZ group except for
the number of observations (NObs=440) and a global replacement
of DZ for MZ. For clarity, the comments at the beginning also should
be changed.
Results of fitting the ACE and ADE models and submodels are summarized
in
Table 6.10.
Table 6.10:
Major
depressive disorder in Virginia adult female twins. Parameter
estimates and goodness-of-fit statistics for models and submodels
including additive genetic (A), common environment (C), random
environment (E), and dominance genetic (D) effects.
| |
Parameter Estimates |
Fit statistics |
| Model |
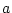 |
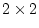 |
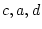 |
 |
 |
df |
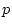 |
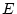 |
-- |
-- |
1.00 |
-- |
56.40 |
2 |
.00 |
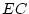 |
-- |
0.58 |
0.81 |
-- |
6.40 |
1 |
.01 |
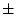 |
0.65 |
-- |
0.76 |
-- |
.15 |
1 |
.70 |
 |
0.65 |
-- |
0.76 |
-- |
.15 |
0 |
-- |
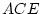 |
0.56 |
-- |
0.75 |
0.36 |
.00 |
0 |
-- |
First, note that the degrees of freedom for fitting to correlation
matrices are fewer than when fitting to covariance matrices. Although
we provide Mx with two correlation matrices, each consisting of 1's on
the diagonal and a correlation on the off-diagonal, the 1's on the
diagonal cannot be considered unique. In fact, only one of them
conveys information which effectively `scales' the covariance. There
is no information in the remaining three 1's on the diagonals of the
MZ and DZ correlation matrices, but Mx does not make this
distinction. Therefore, we must adjust the degrees of freedom by
adding the option Option DFreedom=-3. Another way of looking
at this is that the diagonal 1's convey no information whatsoever, but
that we use one parameter to estimate the diagonal elements (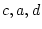 ; it
appears only in the expected variances, not the expected covariances).
Thus, there are 4 imaginary variances and 1 parameter to estimate them
-- giving 3 statistics too many.
Second, the substantive interpretation of the results is that the
model with just random environment fails, indicating significant
familial aggregation for diagnoses of major depressive disorder. The
environmental explanation of familial covariance also fails
(
; it
appears only in the expected variances, not the expected covariances).
Thus, there are 4 imaginary variances and 1 parameter to estimate them
-- giving 3 statistics too many.
Second, the substantive interpretation of the results is that the
model with just random environment fails, indicating significant
familial aggregation for diagnoses of major depressive disorder. The
environmental explanation of familial covariance also fails
(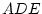 ) but a model of additive genetic and random
environment effects fits well (
) but a model of additive genetic and random
environment effects fits well ( ). There is no possible
room for significant improvement with the addition of any other
parameter, since there are only .15
). There is no possible
room for significant improvement with the addition of any other
parameter, since there are only .15  units left.
Nevertheless, we fitted both ACE and ADE models and found that
dominance genetic effects could account for the remaining variability
whereas shared environmental effects could not. This finding is in
agreement with the observation that the MZ correlation is slightly
greater than twice the DZ correlation. The heritability of liability
to Major Depressive Disorder is moderate but significant at 42%, with
the remaining variability associated with random environmental sources
including error of measurement. These results are not compatible with
the view that shared family experiences such as parental rearing,
social class, or parental loss are key factors in the etiology of
major depression. More modest effects of these factors may be
detected by including them in multivariate model fitting
(Kendler et al., 1992a;
Neale et al., 1992).
Of course, every study has its limitations, and here the primary
limitations are that: (i) the results only apply to females; (ii) the
twin population is not likely to be perfectly representative of the
general population, as it lacks twins who moved out of or into the
state, or failed to respond to initial questionnaire surveys; (iii) a
small number of the twins diagnosed as having major depression may
have had bipolar disorder (manic depression), which may be
etiologically distinct; (iv) the reliance on retrospective reporting
of lifetime mental illness may be subject to bias by either currently
well or currently ill subjects or both; (v) MZ twins may be treated
more similarly as children than DZ twins; and (vi) not all twins were
past the age at risk of first onset of major depression.
Consideration of the first five of these factors is given in
Kendler et al. (1992c). Of
particular note is that a test of limitation (v), the `equal
environments' assumption, was
performed by logistic regression of absolute pair difference of
diagnosis (scored 0 for normal and 1 for affected) on a
quasi-continuous measure of similarity of childhood treatment.
Although MZ twins were on average treated more similarly than DZ
twins, this regression was found to be non-significant. General
methods to handle the effects of zygosity differences in environmental
treatment form part of the class of data-specific models to be
discussed in Section
units left.
Nevertheless, we fitted both ACE and ADE models and found that
dominance genetic effects could account for the remaining variability
whereas shared environmental effects could not. This finding is in
agreement with the observation that the MZ correlation is slightly
greater than twice the DZ correlation. The heritability of liability
to Major Depressive Disorder is moderate but significant at 42%, with
the remaining variability associated with random environmental sources
including error of measurement. These results are not compatible with
the view that shared family experiences such as parental rearing,
social class, or parental loss are key factors in the etiology of
major depression. More modest effects of these factors may be
detected by including them in multivariate model fitting
(Kendler et al., 1992a;
Neale et al., 1992).
Of course, every study has its limitations, and here the primary
limitations are that: (i) the results only apply to females; (ii) the
twin population is not likely to be perfectly representative of the
general population, as it lacks twins who moved out of or into the
state, or failed to respond to initial questionnaire surveys; (iii) a
small number of the twins diagnosed as having major depression may
have had bipolar disorder (manic depression), which may be
etiologically distinct; (iv) the reliance on retrospective reporting
of lifetime mental illness may be subject to bias by either currently
well or currently ill subjects or both; (v) MZ twins may be treated
more similarly as children than DZ twins; and (vi) not all twins were
past the age at risk of first onset of major depression.
Consideration of the first five of these factors is given in
Kendler et al. (1992c). Of
particular note is that a test of limitation (v), the `equal
environments' assumption, was
performed by logistic regression of absolute pair difference of
diagnosis (scored 0 for normal and 1 for affected) on a
quasi-continuous measure of similarity of childhood treatment.
Although MZ twins were on average treated more similarly than DZ
twins, this regression was found to be non-significant. General
methods to handle the effects of zygosity differences in environmental
treatment form part of the class of data-specific models to be
discussed in Section ![[*]](crossref.png) . Overall there was no
marked regression of age on liability to disease in these data,
indicating that correction for the contribution of age to the common
environment is not necessary (see the next section). Variable age at
onset has been considered by Neale et
al. (1989) but a full treatment of this problem is beyond the
scope of this volume. Such methods incorporate not only censoring of
the risk period, but also the genetic architecture of factors involved
in age at onset and their relationship to factors relevant in the
etiology of liability to disease. Note, however, that this problem,
like the problem of measured shared environmental effects, may also be
considered as part of the class of data-specific models.
. Overall there was no
marked regression of age on liability to disease in these data,
indicating that correction for the contribution of age to the common
environment is not necessary (see the next section). Variable age at
onset has been considered by Neale et
al. (1989) but a full treatment of this problem is beyond the
scope of this volume. Such methods incorporate not only censoring of
the risk period, but also the genetic architecture of factors involved
in age at onset and their relationship to factors relevant in the
etiology of liability to disease. Note, however, that this problem,
like the problem of measured shared environmental effects, may also be
considered as part of the class of data-specific models.




Next: 4 Model for Age-Correction
Up: 3 Fitting Genetic Models
Previous: 3 Fitting Genetic Models
Index
Jeff Lessem
2002-03-21
![[*]](footnote.png) .
Contingency tables of MZ and DZ twin pair diagnoses are shown in
Table 6.9.
.
Contingency tables of MZ and DZ twin pair diagnoses are shown in
Table 6.9.
![[*]](crossref.png) on page
on page ![[*]](crossref.png) , except for the title and the dat file used.
, except for the title and the dat file used.
![[*]](crossref.png) . Overall there was no
marked regression of age on liability to disease in these data,
indicating that correction for the contribution of age to the common
environment is not necessary (see the next section). Variable age at
onset has been considered by Neale et
al. (1989) but a full treatment of this problem is beyond the
scope of this volume. Such methods incorporate not only censoring of
the risk period, but also the genetic architecture of factors involved
in age at onset and their relationship to factors relevant in the
etiology of liability to disease. Note, however, that this problem,
like the problem of measured shared environmental effects, may also be
considered as part of the class of data-specific models.
. Overall there was no
marked regression of age on liability to disease in these data,
indicating that correction for the contribution of age to the common
environment is not necessary (see the next section). Variable age at
onset has been considered by Neale et
al. (1989) but a full treatment of this problem is beyond the
scope of this volume. Such methods incorporate not only censoring of
the risk period, but also the genetic architecture of factors involved
in age at onset and their relationship to factors relevant in the
etiology of liability to disease. Note, however, that this problem,
like the problem of measured shared environmental effects, may also be
considered as part of the class of data-specific models.