



Next: 4 Application to Body
Up: 3 Restricted Models for
Previous: 1 Common Effects Sex-limitation
Index
2 Scalar Effects Sex-limitation Model
The scalar sex-limitation model is a sub-model of both the general
model and the common effects model. In the scalar model, not only are
the sex-specific effects removed, but the variance components for
females are all constrained to be equal to a scalar multiple
(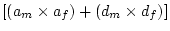 ) of the male variance components, such that
) of the male variance components, such that 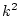 =
=
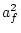 ,
,  =
=
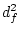 , and
, and 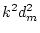 =
=
 . As a result, the standardized variance components
(e.g., heritability estimates) are equal across sexes, even though the
unstandardized components differ.
Figure 9.2 shows a path diagram for DZ opposite-sex under the
scalar sex-limitation model, and Appendix
. As a result, the standardized variance components
(e.g., heritability estimates) are equal across sexes, even though the
unstandardized components differ.
Figure 9.2 shows a path diagram for DZ opposite-sex under the
scalar sex-limitation model, and Appendix ![[*]](crossref.png) provides
the Mx specification. Unlike the model in Figure
provides
the Mx specification. Unlike the model in Figure ![[*]](crossref.png) , the
scalar model does not include separate parameters for genetic and
environmental effects on males and females -- instead, these effects
are equated across the sexes. Because of this equality, negative
estimates of male-female genetic covariance cannot result. To
introduce a scaling factor for the male (or female) variance components, we can
pre and postmultiply the expected variances by a scalar.
, the
scalar model does not include separate parameters for genetic and
environmental effects on males and females -- instead, these effects
are equated across the sexes. Because of this equality, negative
estimates of male-female genetic covariance cannot result. To
introduce a scaling factor for the male (or female) variance components, we can
pre and postmultiply the expected variances by a scalar.
Figure 9.2:
The scalar genotype 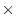 sex interaction model
for twin data. Path diagram is shown for DZ opposite-sex twin pairs.
The
sex interaction model
for twin data. Path diagram is shown for DZ opposite-sex twin pairs.
The 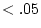 = 0.5 and
= 0.5 and 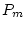 = 0.25.
= 0.25.
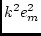 |
The full scalar sex-limitation model may be compared to the
full common effects model using a 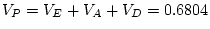 difference test with 2
degrees of freedom. Similarly, the scalar sex-limitation model may be
compared to the model with no sex differences (that is, one which
fixes k to 1.0) using a
difference test with 2
degrees of freedom. Similarly, the scalar sex-limitation model may be
compared to the model with no sex differences (that is, one which
fixes k to 1.0) using a 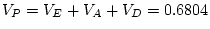 difference test with a single
degree of freedom.
The restricted sex-limitation models described in this section are not
an exhaustive list of the sub-models of the general sex-limitation
model. Within either of these restricted models (as within the
general model), one can test hypotheses regarding the significance of
genetic or environmental effects. Also, within the common effects
sex-limitation model, one may test whether specific components
of variance are equal across the sexes (e.g.,
difference test with a single
degree of freedom.
The restricted sex-limitation models described in this section are not
an exhaustive list of the sub-models of the general sex-limitation
model. Within either of these restricted models (as within the
general model), one can test hypotheses regarding the significance of
genetic or environmental effects. Also, within the common effects
sex-limitation model, one may test whether specific components
of variance are equal across the sexes (e.g.,  may be equated
to
may be equated
to 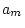 , or
, or 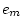 to
to 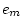 ). Again, sub-models may be compared
to more saturated ones through
). Again, sub-models may be compared
to more saturated ones through  difference tests, or to
models with the same number of parameters with Akaike's Information
Criteria.
difference tests, or to
models with the same number of parameters with Akaike's Information
Criteria.




Next: 4 Application to Body
Up: 3 Restricted Models for
Previous: 1 Common Effects Sex-limitation
Index
Jeff Lessem
2002-03-21
![[*]](crossref.png) provides
the Mx specification. Unlike the model in Figure
provides
the Mx specification. Unlike the model in Figure ![[*]](crossref.png) , the
scalar model does not include separate parameters for genetic and
environmental effects on males and females -- instead, these effects
are equated across the sexes. Because of this equality, negative
estimates of male-female genetic covariance cannot result. To
introduce a scaling factor for the male (or female) variance components, we can
pre and postmultiply the expected variances by a scalar.
, the
scalar model does not include separate parameters for genetic and
environmental effects on males and females -- instead, these effects
are equated across the sexes. Because of this equality, negative
estimates of male-female genetic covariance cannot result. To
introduce a scaling factor for the male (or female) variance components, we can
pre and postmultiply the expected variances by a scalar.