1 General G $\times$ E Interaction Model

First we consider the general G 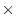$\times$ E interaction model, similar to the general sex-limitation model discussed in section 9.2.3. This model not only allows the magnitude of genetic and environmental effects to vary across environmental conditions, but also, by using information from twin pairs discordant for environmental exposure, enables us to determine whether it is the same set of genes or environmental features that are expressed in the two environments. 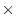Just as we used twins who were discordant for sex (i.e., DZO pairs) to illustrate the sex-limitation model, we use twins discordant for environmental exposure to portray the general G $\times$ E interaction model. Before modeling genetic and environmental effects on these individuals, one must order the twins so that the first of the pair has not been exposed to the putative modifying environment, while the second has (or vice versa, as long as the order is consistent across families and across groups). The path model for the discordant DZ pairs is then identical to that used for the dizygotic opposite-sex pairs in the sex-limitation model; for the discordant MZ pairs, it differs only from the DZ model in the correlation structure of the ultimate genetic variables (see Figure 9.3).

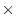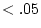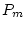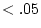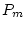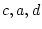Figure 9.3: The general genotype $\times$ environment interaction model for twin data. Path diagram is for MZ and DZ twins discordant for environmental exposure. For MZ pairs, $\alpha$ = 1.0 and $\beta$ = 1.0; for DZ pairs, $\alpha$ = 0.5 and $\beta$ = 0.25. The subscripts $u$ and $e$ identify variables and parameters and unexposed and exposed twins, respectively.

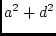Among the ultimate variables in Figure 9.3 are genetic effects that are correlated between the unexposed and exposed twins and those that influence only the latter (i.e., environment-specific effects). For the concordant unexposed and concordant exposed MZ and DZ pairs, path models are comparable to those used for female-female and male-male MZ and DZ pairs in the sex-limitation analysis, with environment-specific effects (instead of sex-specific effects) operating on the exposed twins (instead of the male twins). As a result, the model predicts equal variances within an exposure class, across zygosity groups. In specifying the general G $\times$ E interaction model in Mx, one must again use boundary constraints, in order to avoid negative covariance estimates for the pairs discordant for exposure (Appendix ). Unlike the general sex-limitation analysis, there is enough information in a G $\times$ E analysis to estimate two environment-specific effects. Thus, the magnitude of environment-specific additive and dominant genetic or additive genetic and common environmental effects can be determined. It still is not possible to simultaneously estimate the magnitude of common environmental and dominant genetic effects.