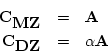Next: 3 Analyzing Genetic and
Up: 4 Multiple Genetic Factor
Previous: 1 Genetic and Environmental
Index
2 Cholesky Decomposition
Clearly, we cannot resolve the genetic and environmental components of
covariance without genetically informative data such as those from
twins. Under our simple AE model we can write, for MZ and DZ pairs,
the expected covariances between the multiple measures of first and
second members very simply:
with the total phenotypic covariance matrix being defined as in
expression 10.4. The coefficient 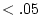 in DZ twins is the
familiar additive genetic correlation between siblings in randomly
mating populations (i.e., 0.5).
The method of maximum likelihood, implemented in Mx, can be used to
estimate A and E. However, there is an important restriction
on the form of these matrices which follows from the fact that they are
covariance matrices: they must be positive definite. It turns out
that if we try to estimate A and E without imposing this
constraint they will very often not be positive definite and thus give
nonsense values (greater than or less than unity) for the genetic and
environmental correlations. It is very simple to impose this constraint
in Mx by recognizing that any positive definite matrix, F, can be
decomposed into the product of a triangular matrix and its
transpose:
in DZ twins is the
familiar additive genetic correlation between siblings in randomly
mating populations (i.e., 0.5).
The method of maximum likelihood, implemented in Mx, can be used to
estimate A and E. However, there is an important restriction
on the form of these matrices which follows from the fact that they are
covariance matrices: they must be positive definite. It turns out
that if we try to estimate A and E without imposing this
constraint they will very often not be positive definite and thus give
nonsense values (greater than or less than unity) for the genetic and
environmental correlations. It is very simple to impose this constraint
in Mx by recognizing that any positive definite matrix, F, can be
decomposed into the product of a triangular matrix and its
transpose:
 |
(65) |
where T is a triangular matrix (i.e., one having fixed zeros in
all elements above the diagonal and free parameters on the diagonal and
below). This is sometimes known as a
triangular decomposition or a Cholesky factorization of
F.
Figure
10.2 shows
this type of model as a path diagram for four variables. In our
case, we represent the genetic and environmental covariance matrices
in Mx by their respective Cholesky factorizations:
 |
(66) |
and
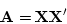 |
(67) |
where X and Z are triangular matrices of additive genetic
and within-family environment factor loadings.
A triangular matrix such as T, X, or Z is square,
having the same number of rows and columns as there are variables.
The first column has non-zero entries in every element; the second has
a zero in the first element and free, non-zero elements everywhere
else, and so on. Thus, the Cholesky factors of F, when F
is a  matrix of the product
matrix of the product  , will have the
form:
, will have the
form:
It is important to recognize that common factor models such as the one
described in Section 10.3 are simply reduced Cholesky models
with the first column of parameters estimated and all others fixed at
zero.




Next: 3 Analyzing Genetic and
Up: 4 Multiple Genetic Factor
Previous: 1 Genetic and Environmental
Index
Jeff Lessem
2002-03-21