



Next: 5 Application to CBC
Up: 2 Models for Multiple
Previous: 3 Biometric Model
Index
We have considered four alternative models for parental ratings of
children's behavior. Each model is for bivariate twin
data where the two variables are the
special case of mothers' ratings and fathers' ratings of the
children's behavior. The least restrictive model, the biometric
model, provides a baseline for comparison with the psychologically
more informative psychometric and bias models. The most restricted
bias model may be formally tested by likelihood ratio
chi-square against either the
psychometric or the unrestricted bias models. However, these latter
two are not themselves nested. The relationships between these
models, without taking into account sex limitations, are summarized in
Figure 11.4. In this figure the solid arrows
Figure 11.4:
Diagram of nesting of biometric, psychometric, and rater bias
models.
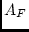 |
represent the process of constraining a more general model to yield a
more restrictive model; the model at the arrow head is nested within
the model at the tail of the arrow and may be tested against it by a
likelihood ratio chi square. The dashed arrows represent rotational
constraints on the biometric model. The nine parameter psychometric
model requires, for example, that the covariance between maternal and
paternal ratings be no greater than the variance of either type of
rating; in factor analytic terms this would require a constrained
rotation of the biometric model solution. The ten parameter
psychometric model, allowing  not equal to unity, still
imposes the constraints that the contributions of the common
influences to the variance of maternal ratings, the variance of
paternal ratings, and the covariance between them be in the ratio
not equal to unity, still
imposes the constraints that the contributions of the common
influences to the variance of maternal ratings, the variance of
paternal ratings, and the covariance between them be in the ratio
 for each source of influence. Thus, even though
this model has 10 parameters (and hence is not identified for
bivariate twin data) any of its solutions, arrived at by fixing one of
the parameters to an arbitrary value, will again represent in factor
analytic terms a constrained rotation of the biometric model.
for each source of influence. Thus, even though
this model has 10 parameters (and hence is not identified for
bivariate twin data) any of its solutions, arrived at by fixing one of
the parameters to an arbitrary value, will again represent in factor
analytic terms a constrained rotation of the biometric model.




Next: 5 Application to CBC
Up: 2 Models for Multiple
Previous: 3 Biometric Model
Index
Jeff Lessem
2002-03-21