



Next: 4 Preparing Raw Data
Up: 3 Ordinal Data Analysis
Previous: 4 Terminology for Types
Index
5 Using PRELIS with Ordinal Data
Here we give a PRELIS script to read only two from a long list of psychiatric
diagnoses, coded as 1 or 0 in these data.
Diagnoses and age MZ twins: VARIABLES ARE:
DEPLN4 DEPLN2 DEPLN1 DEPLB4 DEPLB2 DEPLB1 GADLN6 GADLN1
GADLB6 GADLB1 GAD88B GAD88N PANN PANB PHON PHOB ETOHN
ETOHB ANON ANOB BULN BULB DEPLN4T2 DEPLN2T2 DEPLN1T2
DEPLB4T2 DEPLB2T2 DEPLB1T2 GADLN6T2 GADLN1T2 GADLB6T2
GADLB1T2 GAD88BT2 GAD88NT2 PANNT2 PANBT2 PHONT2 PHOBT2
ETOHNT2 ETOHBT2 ANONT2 ANOBT2 BULNT2 BULBT2/
FORMAT IN FULL IS:
(2X, F8.2,F1.0, 43(1X,F1.0)
Diagnoses and age MZ twins
DA NI=3 NO=0
LA; DOB DEPLN4 DEPLN4T2
RA FI=DIAGMZ.DAT FO
(2X, F8.2,F1.0, 43x,F1.0)
OR DEPLN4-DEPLN4T2
OU MA=PM SM=DEPLN4MZ.COR SA=DEPLN4MZ.ASY PA
Diagnoses and age DZ twins
DA NI=3 NO=0
LA; DOB DEPLN4 DEPLN4T2
RA FI=DIAGdZ.DAT FO
(2X, F8.2,F1.0, 43x,F1.0)
OR DEPLN4-DEPLN4T2
OU MA=PM SM=DEPLN4dZ.COR SA=DEPLN4dZ.ASY PA
Note that again we have used the
FORTRAN format to control which variables are read. One key difference from
the continuous case is the
use of MA=PM, which requests calculation of a matrix of polychoric,
polyserial and product moment correlations. The program uses product moment
correlations when both variables are continuous, a polyserial (or biserial)
when one is ordinal and the other continuous, and a polychoric (or
tetrachoric) when both
are ordinal.
Running the script
produces four output files
DEPLN4MZ.COR, DEPLN4MZ.ASY, DEPLN4DZ.COR and
DEPLN4DZ.ASY which may be read directly into Mx using
PMatrix and ACov
commands. Notice that we have `stacked' two scripts in one file, one to read
and compute statistics from the MZ data file (FI=DIAGMZ.DAT) and a
second to do the same thing for the DZ data. Also notice that
the SM command is used to output the correlation matrix
and SA is to save the asymptotic weight
matrix. In fact, PRELIS saves the weight matrix multiplied by the sample size
which is what Mx expects to receive when the ACov command is used.
The PA command requests that the asymptotic weight matrix itself be
printed in the output. However, PRELIS saves this file in a binary
format which must be converted to ASCII for use with Mx. The utility
bin2asc, supplied with PRELIS, can be used for this purpose.
In the
PRELIS output, there are a number of summary statistics for continuous
variables (means and standard deviations, and histograms) and frequency distributions with
bar graphs, for the ordinal variables. To provide the user with some
guide to the origin of statistics describing the covariance between variables,
PRELIS prints means and standard deviations of continuous variables separately
for each category of each pair of ordinal variables, and contingency tables between each
ordinal variables. Towards the end of the output there is a table printed with
the following format:
TEST OF MODEL
CORRELATION CHI-SQU. D.F. P-VALUE
___________ ________ ____ _______
DEPLN4 VS. DOB -.233 (PS) 5.067 1 .024
DEPLN4T2 VS. DOB .010 (PS) 6.703 1 .010
There are two quite different chi-squared tests printed on the output.
The first, under TEST OF MODEL is a test of the goodness of fit
of the bivariate normal distribution model to the data. In the case
of two ordinal variables with 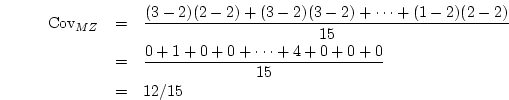 and
and 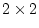 categories in each, there
are
categories in each, there
are  df as described in expression 2.5 above.
Likewise there will be
df as described in expression 2.5 above.
Likewise there will be 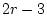 df for the continuous by ordinal
statistics, as described in expression 2.6. If the
df for the continuous by ordinal
statistics, as described in expression 2.6. If the 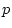 -value
reported by PRELIS is low (e.g.
-value
reported by PRELIS is low (e.g.  ), then concern arises about
whether the bivariate normal distribution model is appropriate for
these data. For a polyserial correlation (correlations between
ordinal and continuous variables), it
may simply be that the continuous variable is not normally
distributed, or that the association between the variables does not
follow a bivariate normal distribution. For polychoric
correlations, there is no univariate
test of normality involved, so failure of the model would imply that
the latent liability distributions do not follow a bivariate normal.
Remember however that significance levels for these tests are not
often the reported
), then concern arises about
whether the bivariate normal distribution model is appropriate for
these data. For a polyserial correlation (correlations between
ordinal and continuous variables), it
may simply be that the continuous variable is not normally
distributed, or that the association between the variables does not
follow a bivariate normal distribution. For polychoric
correlations, there is no univariate
test of normality involved, so failure of the model would imply that
the latent liability distributions do not follow a bivariate normal.
Remember however that significance levels for these tests are not
often the reported 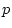 -value, because we are performing multiple
tests. If the tests were independent, then with
-value, because we are performing multiple
tests. If the tests were independent, then with 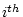 such tests the
such tests the
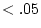 significance level would not be the reported
significance level would not be the reported 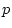 -value but
-value but
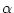 . Therefore concern would arise only if
. Therefore concern would arise only if 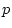 was very small
and a large number of tests had been performed. In our case, the
tests are not independent because, for example, the correlation of A
and B is not independent of the correlation of A and C, so the
attenuation of the
was very small
and a large number of tests had been performed. In our case, the
tests are not independent because, for example, the correlation of A
and B is not independent of the correlation of A and C, so the
attenuation of the 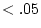 level of significance is not so extreme as
the
level of significance is not so extreme as
the 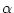 formula predicts. The amount of attenuation will be
application specific, but would often be closer to
formula predicts. The amount of attenuation will be
application specific, but would often be closer to 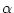 than
simply to
than
simply to 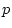 .
The second chi-squared statistic printed by PRELIS (not shown in the above
sample of output) tests whether the
correlation is significantly different from zero. A similar result should be
obtained if the summary statistics are supplied to Mx, and a chi-squared
difference test (see Chapter
.
The second chi-squared statistic printed by PRELIS (not shown in the above
sample of output) tests whether the
correlation is significantly different from zero. A similar result should be
obtained if the summary statistics are supplied to Mx, and a chi-squared
difference test (see Chapter ![[*]](crossref.png) ) is performed between a
model which allows the correlation to be a free parameter, and one in
which the correlation is set to zero.
The use of weight matrices as input to Mx is
described elsewhere in this
book. Here we have described the generation of a weight matrix for a
correlation matrix, but it is also possible to use weight matrices for
covariance matrices
) is performed between a
model which allows the correlation to be a free parameter, and one in
which the correlation is set to zero.
The use of weight matrices as input to Mx is
described elsewhere in this
book. Here we have described the generation of a weight matrix for a
correlation matrix, but it is also possible to use weight matrices for
covariance matrices![[*]](footnote.png) .
Both methods are part of the asymptotically distribution free (ADF)
methods pioneered
by Browne (1984). It is not yet clear whether maximum
likelihood or ADF methods are generally better for coping with data that are
not multinormally distributed; further simulation studies are required. The
ADF methods require more numerical effort and become cumbersome to use with
large numbers of variables. This is so because the size of the weight matrix
rapidly increases with number of variables. The number of elements on and
below the diagonal of a matrix is a triangular number given by
.
Both methods are part of the asymptotically distribution free (ADF)
methods pioneered
by Browne (1984). It is not yet clear whether maximum
likelihood or ADF methods are generally better for coping with data that are
not multinormally distributed; further simulation studies are required. The
ADF methods require more numerical effort and become cumbersome to use with
large numbers of variables. This is so because the size of the weight matrix
rapidly increases with number of variables. The number of elements on and
below the diagonal of a matrix is a triangular number given by
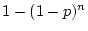 . The number of elements in this weight matrix is a triangular
number of a triangular number, or
. The number of elements in this weight matrix is a triangular
number of a triangular number, or
In the case of correlation matrices, the number
of elements is somewhat less, but still increases as a quadratic function:
As a compromise when the number of variables
is large, Jöreskog and Sörbom suggest the use of
diagonal weights, i.e. just the variances of the correlations and not their
covariances. However, tests of significance are likely to be inaccurate with
this method and estimates of anything other than the full or true
model would be biased.




Next: 4 Preparing Raw Data
Up: 3 Ordinal Data Analysis
Previous: 4 Terminology for Types
Index
Jeff Lessem
2002-03-21
 and
and ![[*]](crossref.png) ) is performed between a
model which allows the correlation to be a free parameter, and one in
which the correlation is set to zero.
The use of weight matrices as input to Mx is
described elsewhere in this
book. Here we have described the generation of a weight matrix for a
correlation matrix, but it is also possible to use weight matrices for
covariance matrices
) is performed between a
model which allows the correlation to be a free parameter, and one in
which the correlation is set to zero.
The use of weight matrices as input to Mx is
described elsewhere in this
book. Here we have described the generation of a weight matrix for a
correlation matrix, but it is also possible to use weight matrices for
covariance matrices![[*]](footnote.png) .
Both methods are part of the asymptotically distribution free (ADF)
methods pioneered
by Browne (1984). It is not yet clear whether maximum
likelihood or ADF methods are generally better for coping with data that are
not multinormally distributed; further simulation studies are required. The
ADF methods require more numerical effort and become cumbersome to use with
large numbers of variables. This is so because the size of the weight matrix
rapidly increases with number of variables. The number of elements on and
below the diagonal of a matrix is a triangular number given by
.
Both methods are part of the asymptotically distribution free (ADF)
methods pioneered
by Browne (1984). It is not yet clear whether maximum
likelihood or ADF methods are generally better for coping with data that are
not multinormally distributed; further simulation studies are required. The
ADF methods require more numerical effort and become cumbersome to use with
large numbers of variables. This is so because the size of the weight matrix
rapidly increases with number of variables. The number of elements on and
below the diagonal of a matrix is a triangular number given by