- ... meioses
![[*]](footnote.png)
- meiosis is the process of
gametogenesis in which either sperm or ova are formed
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
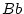
![[*]](footnote.png)
- This notation is described more fully in
Chapter 3.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... environment
![[*]](footnote.png)
- Twins born
serially by embryo implantation are currently far too rare for the
purposes of statistical distinction between pre- and post-natal
effects!
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... twins
![[*]](footnote.png)
- These data are for illustration only; they would normally be treated as ordinal, not continuous, and would be
summarized differently, as described in Section 2.3. Note also that
we do not need to have equal numbers of pairs in the two groups.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... pair
![[*]](footnote.png)
- It is possible to use data files that
contain both types of twins and some code to discriminate between them, but it
is less efficient.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... table
![[*]](footnote.png)
- Mathematically
these expected proportions can be written as double integrals. We do not
explicitly define them here, but return to the subject in the context of
ascertainment discussed in Chapter
![[*]](crossref.png)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... inheritance"
![[*]](footnote.png)
- In fact quite a small
number of genetic factors may give rise to a distribution which is for almost
all practical purposes indistinguishable from a normal distribution
[Kendler and Kidd, 1986].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... matrices
![[*]](footnote.png)
- The number of elements in a weight matrix for a
covariance matrix is greater than that for a correlation matrix. For this
reason, it is necessary to specify
Matrix=PMatrix on the Data line
of a Mx job that is to read a weight matrix.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... inches
![[*]](footnote.png)
- Note: 1 inch =
2.54cm; 1 foot = 12 inches.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... mean
![[*]](footnote.png)
- This is an application of the method described in
Section 2.2.1. It looks a bit more intimidating here because
of (a) the multiplication by the frequency, and (b) the use of letters
not numbers. To gain confidence in this method, the reader may wish
to choose values for
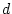 and
and  and work through an example.
and work through an example.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
transpose
![[*]](footnote.png)
- Transposition is defined in Section 4.3.2
below. Essentially the rows become columns and vice versa.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... above
![[*]](footnote.png)
- Those readers wishing to
know more about the uses of eigenvalues and eigenvectors may consult
Searle (1982) or any general text on matrix algebra.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... matrices
![[*]](footnote.png)
- N.B. For a
diagonal matrix one takes the reciprocal of only the diagonal
elements!
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... variables,
![[*]](footnote.png)
- Multivariate
path diagrams, including delta path [van Eerdewegh, 1982], copath
[Cloninger, 1980], and conditional path diagrams [Carey, 1986a]
employ slightly different rules, but are outside the scope of this
book. See Vogler (1985) for a general description.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
relationship
![[*]](footnote.png)
- i.e. we do not expect different heritabilities
for twin 1 and twin 2; however for other relationships such as
parents and children, the assumption may not be valid, as could be
established empirically if we had genetically informative data in
both generations.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... exists
![[*]](footnote.png)
- The reader
may like to verify this by calculating the determinant according to
the method laid out in Section 4.3.2 or with the aid of a
computer.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... sum
![[*]](footnote.png)
- i.e. the unsigned
difference between twin 1 and twin 2 of each pair,
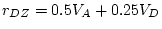 with
with
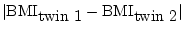
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...gill81
![[*]](footnote.png)
- small
observed variances (
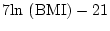 ) can be problematic as the predicted
covariance matrix may become non-positive definite.
) can be problematic as the predicted
covariance matrix may become non-positive definite.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... matrix
![[*]](footnote.png)
- A
singular matrix cannot be inverted (see Chapter 4) and,
therefore, the maximum likelihood fit function (see
Chapter
![[*]](crossref.png) ) cannot be computed.
) cannot be computed.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... freedom
![[*]](footnote.png)
- The degrees of
freedom associated with this test are calculated as the difference
between the number of observed statistics (
 ) and the number of
estimated parameters (
) and the number of
estimated parameters ( ) in the model. Our data consist of two
variances and a covariance for each of the MZ and DZ groups, giving
) in the model. Our data consist of two
variances and a covariance for each of the MZ and DZ groups, giving
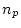 in total. The CE model has two parameters
in total. The CE model has two parameters 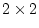 and
and 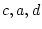 , so
, so
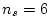 df.
df.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... phenotypes)
![[*]](footnote.png)
- Except where explicitly noted,
all models presented in this text treat observed variables as
deviation phenotypes.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
category
![[*]](footnote.png)
- Excessive contributions to the
 by a small
number of outliers could also be detected by fitting models directly
to the raw data using Mx. Though a more powerful method of
assessing the impact of outliers, it is beyond the scope of this
volume.
by a small
number of outliers could also be detected by fitting models directly
to the raw data using Mx. Though a more powerful method of
assessing the impact of outliers, it is beyond the scope of this
volume.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
assessments
![[*]](footnote.png)
- Such independent assessments would risk retest
effects if they were close together in time. Conversely,
assessments separated by a long interval would risk actual
phenotypic change from one occasion to the next. For a
methodological review of this area, see Helzer
(1977)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
variance
![[*]](footnote.png)
- The reader might like to consider what the
components of this shared variance might include in these data
obtained from the mothers of the twins and think forward to our
treatment of rating data in Chapter 11.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... effects
![[*]](footnote.png)
- The reasoning goes like
this: (e.g.) males have a elevated level of a chemical that prevents
any gene expression from certain loci, at random with respect
to the phenotype under study. Thus, both additive and dominant
genetic effects would be reduced in males vs females, and hence the
same genetic correlation between the sexes would apply to both.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... data
![[*]](footnote.png)
- In exploratory factor analysis the
term ``factor structure'' is used to describe the correlations
between variables and factors, but in confirmatory analysis, as
described here, the term often describes the characteristics of a
hypothesized factor model.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... 1989)
![[*]](footnote.png)
- We are grateful to Dr. Richard
Schieken for making these data, gathered as part of a project
supported by NHLBI award HL-31010, available prior to publication.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...)
![[*]](footnote.png)
- This problem is extreme when maximum likelihood is
the fit function, because the inverse of
 is required (see
Chapter
is required (see
Chapter ![[*]](crossref.png) ).
).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... adequately
![[*]](footnote.png)
- There are in fact some other special cases
such as scalar sex-limitation - where identical genetic or
environmental factors may have different factor loadings for males
and females -- when the psychometric model may fit as well or
better than the biometric model.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... sex-limitation
![[*]](footnote.png)
- This is to avoid
estimated loadings of opposite sign in boys and girls - see
Chapter 9.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... children
![[*]](footnote.png)
- However, if these effects were
substantial and if MZ twins correlated more highly than DZ twins in
their interactional style, the variance of parents' ratings should
differ (Neale et al., 1992). Given
sufficient sample size, these effects would lead to failure of these
models.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
![[*]](footnote.png)
![[*]](footnote.png)
![[*]](footnote.png)
![[*]](footnote.png)
![[*]](footnote.png)
![[*]](footnote.png)
![[*]](crossref.png)
![[*]](footnote.png)
![[*]](footnote.png)
![[*]](footnote.png)
![[*]](footnote.png)
![[*]](footnote.png)
![[*]](footnote.png)
![[*]](footnote.png)
![[*]](footnote.png)
![[*]](footnote.png)
![[*]](footnote.png)
![[*]](footnote.png)
![[*]](footnote.png)
![[*]](footnote.png)
![[*]](crossref.png) ) cannot be computed.
) cannot be computed.
![[*]](footnote.png)
![[*]](footnote.png)
![[*]](footnote.png)
![[*]](footnote.png)
![[*]](footnote.png)
![[*]](footnote.png)
![[*]](footnote.png)
![[*]](footnote.png)
![[*]](footnote.png)
 is required (see
Chapter
is required (see
Chapter ![[*]](crossref.png) ).
).
![[*]](footnote.png)
![[*]](footnote.png)
![[*]](footnote.png)