



Next: 6 Univariate Analysis
Up: 5 Path Analysis and
Previous: 7 Identification of Models
Index
In this chapter we have reviewed briefly the use of path analysis to
represent certain linear and genetic models. We have discussed the
conventions of path analysis, and shown how it may be used to derive
the covariance matrices predicted under a particular model. We
emphasize that the systems described here have been chosen as simple
examples to illustrate elementary principles of path analysis.
Although these examples are somewhat simplistic in the sense that they
do not elucidate many of the characteristics of which structural
equation models are capable, familiarity with them should provide
sufficient skills for comprehension of other, more advanced, genetic
models described in this text and for development of one's own path
models.
However, one aspect of structural models which has not been discussed
in this chapter is that of multiple indicators. While not strictly a feature of path analysis, multiple
indicator models, -- those with more than one measure for each
dependent or independent variable -- warrant some attention because
they are used often in genetic analyses of twin data, and in analyses
of behavioral data in general. Our initial regression examples from
Figure 5.2 assumed that we had only a
single measure for each variable (systolic blood pressure, sodium
intake, etc), and could ignore measurement error in these observed variables. Inclusion of multiple
indicators allows for explicit representation of assumptions about
measurement error in a model. In our regression example of
Figures 5.2d and e, for example, we might have
several measures of our independent (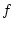 ) variables, a number of
measures of sodium intake (e.g., diet diary and urinary sodium),
multiple measures of exercise (e.g., exercise diary and frequency
checklist), and numerous measures of obesity (e.g., self-report body
mass index, measures of skinfold thickness). Likewise, we might have
many estimates of our dependent
) variables, a number of
measures of sodium intake (e.g., diet diary and urinary sodium),
multiple measures of exercise (e.g., exercise diary and frequency
checklist), and numerous measures of obesity (e.g., self-report body
mass index, measures of skinfold thickness). Likewise, we might have
many estimates of our dependent 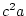 variables, such as repeated
measures of blood pressure, and several tests for coronary artery
disease. Figure 5.4 expands Figure 5.2a by
illustrating the cases of (a) one variable per construct, (b) two
variables per construct, and (c) three or more observed variables
per construct.
variables, such as repeated
measures of blood pressure, and several tests for coronary artery
disease. Figure 5.4 expands Figure 5.2a by
illustrating the cases of (a) one variable per construct, (b) two
variables per construct, and (c) three or more observed variables
per construct.
Figure 5.4:
Regression path models with multiple indicators.
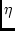 |
Covariance and variance expectations for multiple indicator models
such as those shown in Figure 5.4 follow without exception
from the path tracing rules outlined earlier in this chapter.
However, the increase in number of variables in these models often
results in substantial increases in model complexity. One of the
important attractions of Mx is its flexibility in specifying models
using matrix algebra. Various commands are available that allow
changing the number of variables with relative ease.
It is to the Mx model specification that we now turn.




Next: 6 Univariate Analysis
Up: 5 Path Analysis and
Previous: 7 Identification of Models
Index
Jeff Lessem
2002-03-21